
- Ordering Rounding and Order of Operations
- Home
- Introduction to Inequalities
- Comparing a Numerical Expression With a Number
- Ordering Large Numbers
- Rounding to Tens or Hundreds
- Rounding to Hundreds or Thousands
- Rounding to Thousands, Ten Thousand, or Hundred Thousand
- Estimating a Sum of Whole Numbers
- Estimating a Difference of Whole Numbers
- Estimating a Product of Whole Numbers
- Estimating a Quotient of Whole Numbers
- Writing Expressions Using Exponents
- Introduction to Exponents
- Power of 10: Positive Exponent
- Power of 10: Negative Exponent
- Introduction to Parentheses
- Comparing Numerical Expressions With Parentheses
- Introduction to Order of Operations
- Order of Operations With Whole Numbers
- Order of Operations With Whole Numbers and Grouping Symbols
- Order of Operations With Whole Numbers and Exponents: Basic
Power of 10: Negative Exponent
In this lesson, we deal with problems involving expressions with 10 as base having negative exponents.
Rules to find the negative exponent of 10
Suppose we have an expression having 10-n.
In normal course the value of 10-n is found by multiplying the base
10 'n' times in the denominator and putting a 1 in the numerator.We use a shortcut to solve such problem. We look at the exponent and then write a decimal point followed by as many zeros as one less than exponent and a 1.
Evaluate 10-3
Solution
Step 1:
Here we have an expression involving power of ten with a negative exponent.
The base is 10 and the exponent is −3.
Step 2:
In normal course the value of 10-3 can be found by multiplying the base 10 three times in the denominator and putting a 1 in the numerator.
10-3 = 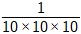 = 0.001
= 0.001
Step 3:
Using a shortcut, we find that the exponent is -3. We write a decimal point followed by two (1 less than 3) zeros and a 1.
So 10-3 = 0.001
Evaluate 10-5
Solution
Step 1:
Here we have an expression involving power of ten with a negative exponent.
The base is 10 and the exponent is −5.
Step 2:
In normal course the value of 10-5 is found by multiplying the base 10 five times in the denominator and putting a 1 in the numerator.
10-5 = 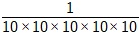 = 0.00001
= 0.00001
Step 3:
Using a shortcut, we find the exponent is -5. We write a decimal point followed by four (1 less than 5)zeros and a 1.
So 10-5 = 0.00001