Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is SLR (1) Parser?
SLR represents "Simple LR Parser". It is very simple and economical to execute. But it fails to make a parsing table for some class of grammars, i.e., why CLR and LALR are used which implements mainly all class or type of grammars. It constructs parsing tables which helps to perform parsing of input strings.
SLR(1) − A grammar having an SLR parsing table is said to be SLR (1).
Working of SLR Parser
SLR Parsing can be done if context-free Grammar will be given. In LR (0), 0 means there is no Look Ahead symbol.
The Canonical collection of LR (0) items
The LR (0) item for Grammar G consists of a production in which symbol dot (.) is inserted at some position in R.H.S of production.
For Example − For the production S → ABC, the generated LR (0) items will be −
S →∙ ABC
S → A ∙ BC
S → AB ∙ C
S → ABC ∙
Production S → ε generates only one item, i.e., S →∙
Canonical LR (0) collection helps to construct LR parser called Simple LR (SLR) parser.
To create Canonical LR (0) collection for Grammar, 3 things are required −
- Augmented Grammar
- Closure Function
- goto Function
Augmented Grammar − If grammar G has start symbol S, then augmented Grammar is new Grammar G′ with new start symbol S′. Also, it will contain the production S′ → S.
Closure − For a Context-Free Grammar G, if I is the set of items or states of grammar G, then −
Every item in I is in the closure (I).
If rule A → α. B β is a rule in closure (I) and there is another rule for B such as B → γ then closure (I) will consist of A → α. Bβ and B → . γ
goto (I, X) − If there is a production A → α ∙ X β in I then goto (I, X) is defined as closure of the set of items of A → α X ∙ β where I is set of items and X is grammar symbol (non-terminal).
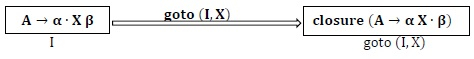
Construction of SLR Parsing Table
There are basically two parts of SLR Parsing table
- Action
- goto
Action and goto table can be filled using the following Algorithm −
Algorithm
Input − An Augmented Grammar G′
Output − SLR Parsing Table
Method
Initially construct set of items
C = {I0, I1, I2 … … In} where C is a set of LR (0) items for Grammar.
Parsing actions are based on each item or state I1.
Various Actions are −
- If A → α ∙ a β is in Ii and goto (Ii, a) = Ij then set Action [i, a] = shift j".
- If A → α ∙ is in Ii then set Action [i, a] to "reduce A → α" for all symbol a, where a ∈ FOLLOW (A).
- If S′ → S ∙ is in Ii then the entry in action table Action [i, $] = accept".
The goto part of the SLR table can be filled as− The goto transition for the state i is considered for non-terminals only. If goto (Ii, A) = Ij then goto [i, A] = j
All entries not defined by rules 2 and 3 are considered to be "error. "
5K+ Views
