Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Show that every SLR (1) is unambiguous, but some unambiguous grammars are not SLR (1). Check this for the following productions.
S → L = R
S → R
L →* R
L → id
R → L
Solution
Step1 − First of all, convert it into augmented grammar G′ and number the productions
(0) S′ → S
(1) S → L = R
(2) S → R
(3) L →∗ R
(4) L → id
(5) R → L
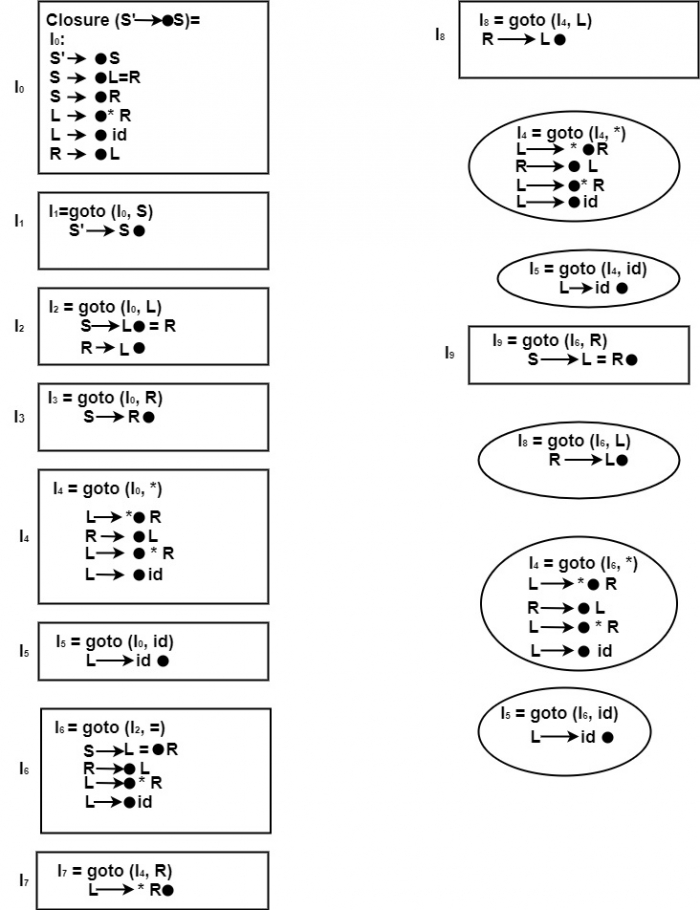
Step2 − Find closure and goto function to construct LR (0) items.
In the following set of LR (0) items, Boxes represents the new states and circle represents Repeating states
Step3− Computation of FOLLOW− Applying Rule (1) of FOLLOW, we get
FOLLOW(S) = $ (1)
- S → L = R
Applying Rule (2) FOLLOW − Comparing S → L = R with A → α B β.
| S → | Ε | L | = R |
| A → | Α | B | Β |
∴ A = S, α = ε, B = L, β = {= R}
FIRST(β) = FIRST(= R) = {=} does not contain ε
Rule (2a) of FOLLOW
FOLLOW(L) = {=} (2)
Applying Rule (3) of FOLLOW− Comparing S → L = R with A → α B
| S → | L = | R |
| A → | α | Β |
∴ FOLLOW(R) = {FOLLOW(S)} (3)
- S → R
Rule (2) of FOLLOW cannot be applied.
As S → R cannot be compared with A → α B β. Because, if we compare, we get, α = ε, B = R, β = ε. But β should not be ε to apply this rule.
Applying Rule (3) of FOLLOW − Comparing S → R with A → α B
| S → | ε | R |
| A → | α | Β |
∴ A = S, α = ε, B = R
FOLLOW(R) = {FOLLOW(S)} (4)
- L →*R
Rule (2) of FOLLOW cannot be applied.
As L →* R cannot be compared with A → α B β. Since β will be ε, which is not possible.
Applying Rule (3) of FOLLOW − Comparing L →∗ R with A → α B
| L → | * | R |
| A → | α | Β |
∴ A = L, α =∗, B = R
FOLLOW(R) = {FOLLOW(L)} (5)
- L →id
Rule (2) and (3) of FOLLOW cannot be applied.
As L → id cannot be match with A → α B β and A → α B.
- R → L
Rule (2) cannot be applied.
As R → L cannot be match with A → α B β.
Applying Rule (3) of FOLLOW − Comparing R → L with A → α B
| R → | E | L |
| A → | A | Β |
∴ A = R, α = ε, B = L
FOLLOW(L) = {FOLLOW(R)} (6)
Combining Statements (1) to (6)
FOLLOW(S) = $ (1)
FOLLOW(L) = {=} (2)
FOLLOW(R) = {FOLLOW(S)} (3)
FOLLOW(R) = {FOLLOW(S)} (4)
FOLLOW(R) = {FOLLOW(L)} (5)
FOLLOW(L) = {FOLLOW(R)} (6)
From (1)
FOLLOW(S) = $
From (1), (2), (3), (4), (5), (6).
FOLLOW(L) = FOLLOW(R) = {=, $}
Construction of Parsing Table
Filling Shift Entries (s)
Since goto (I0,*) = I4
∴ Action [0,∗] = s4
Since goto (I0, id) = I5
∴ Action [0, id] = s5
Similarly, All shift entries (s) are filled into the table.
Filling Reduce Entries (r)
Applying Rule (2b) construction of SLR Parsing Table
Consider
I2 S → L ∙= R
R → L ∙
R → L ∙ is compared with A → α ∙
| R → | L | . |
| A → | α | . |
∴ A = R, α = L
Since R → L is Production number (5) in the given Question.
∴ Write r5 in front of Row state 2 and column =, $.
Similarly, other entries of Reduce are filled into the table.
Filling of "accept" Entry
Consider I1
I1 − S′ → S ∙
Apply Rule (4) of Parsing Table Construction
∴ Write “accept” in front of row state 1 and column $.
By Filling all the shift, reduce, goto & accept entries, we get the following Parsing Table.
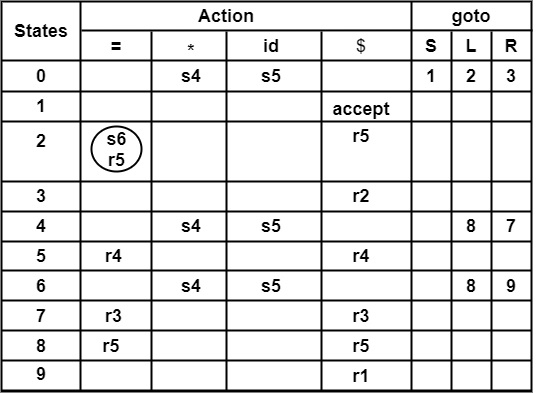
The following table display precisely that there are multiple entries in Action [2, =] = s6 or r5.
State I2 − S → L ∙ = R
R → L ∙
R → L ∙ is of form A → α ∙
∴ Reduce Rule can be applied on it.
R → L is production number (5) in given question.
∴ Action [2, =] = r5
∴ goto (I2, =) = I6
∴ Action [2, =] = s6
Therefore, there is shift | Reduce conflict on Entry Action [2, =]. This shows that given grammar is not SLR (1).
2K+ Views
