Sum of minimum element at each depth of a given non cycle graph

A graph that does not contain any cycles or loops is called a non-cycle graph. A tree is a non-cycle graph in which every node is joined to another unique node. A non-cycle graph is also known as an acyclic graph.

Difference between cycle graph and non-cycle graph −

Cycle Graph	Non-Cycle graph
The graph forms a closed loop.	The graph doesn’t form a closed loop.
The graph doesn’t contain a depth loop	The graph contains each depth.

Example 1

let’s take an example of a cycle graph −

A Cycle graph is formed when the closed loop is existing.

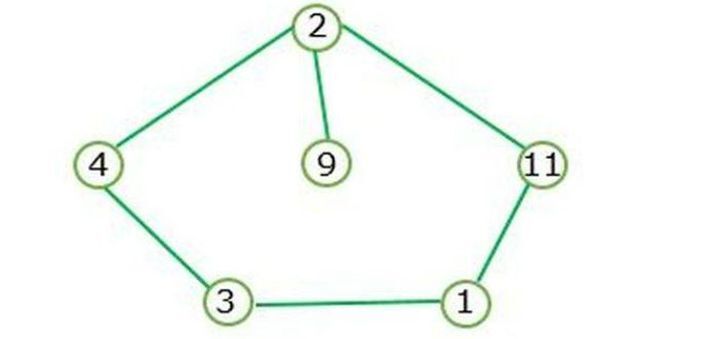
Figure I represents the cycle graph and doesn’t contain the depth node.

Example 2

Let’s take an example of a non-cycle graph −

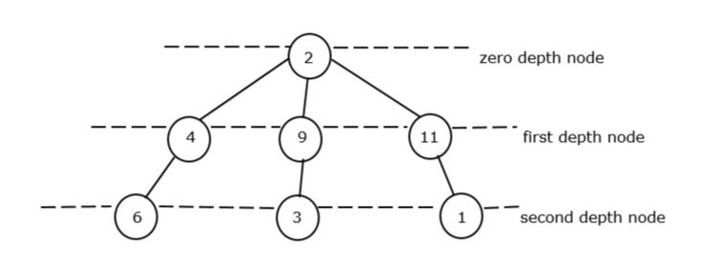
The root node of the tree is known as the zero-depth node. In Figure II, at zero depth there is only one root i.e, 2. So it is considered a minimum depth node of zero.

In the first depth node, we have 3 node elements like 4, 9, and 1 but the minimum element is 4.

In the second depth node, we have again 3 node elements like 6, 3, and 1 but the minimum element is 1.

We will know how the total depth node is derived,

Total depth node = min of zero_depth node + min of first_depth node + min of zero_depth node

Total depth node = 2 + 4 + 3 = 9. So, 9 is the total minimum sum of a non-cycle graph.

Syntax

The following syntax used in the program:
struct name_of_structure{
   data_type var_name;   
   // data member or field of the structure.
}

• struct − This keyword is used to represent structure datatype.

• name_of_structure − We are providing any name to the structure.

• The structure is a collection of various related variables in one place.

Queue < pair < datatype, datatype> > queue_of_pair

make_pair() 

Parameters

The queue of pairs in C++ −

• This is the general STL template of a queue of pairs to combine the two different datatypes and the queue pair comes under the utility header file.

• Queue_of_pair − We are giving any name to the pair.

• make_pair() − This is used to construct a pair object with two elements.

name_of_queue.push()

Parameters

• name_of_queue − We are naming the queue name.

• push() − This is a predefined method that comes under the queue header and the use of push method is to insert the element or values.

name_of_queue.pop()

Parameters

• name_of_queue − We are naming the queue name.

• pop() − This is a predefined method that comes under the queue header file and the use of pop method is to delete the entire element or values.

Algorithm

• We will start the program header file namely ‘iostream’, ‘climits’, ‘utility’, and ‘queue’.

• We are creating the structure ‘tree_node’ with integer value ‘val’ for taking node values. Then we create the tree_node pointer with the given data to initialize the left and right child nodes to store the values. Next, we create a tree_node function where int x is passed as a parameter and verify it for equivalent to a ‘val’ integer and assign the left and right child node to null.

• Now we will define a function minimum_sum_at_each_depth() which accepts an integer value as a parameter to finding the minimum sum of each depth. Using the if- statement it checks if the root value of a tree is null then it returns 0.

• We are creating queue pair of STL(standard template library) to combine two values.

• We have created a queue variable named q as pair that will perform two methods i.e. push() and make_pair(). Using both these methods we are inserting the values and construct the two pairs of an object.

• We are initializing the three variables namely ‘present_depth’, ‘present_sum’, and ‘totalSum’ which will be used for further finding the present sum as well as finding the total minimum sum.

• After initializing variables, we create a while loop to check the condition if the queue pair is not empty then the counting of nodes will start from the beginning. Next, we use the ‘pop()’ method to delete an existing node because it will move to the next depth of the tree to calculate the minimum sum.

• Now we will create three if-statement to return the total minimum sum.

• Following that we will start the main function and structure the tree format of the input pattern with the help of root pointer, left, and right child nodes respectively, and pass the node values through new ‘tree_node’.

• Finally, we call the ‘minimum_sum_at_each_depth(root)’ function and pass the parameter root to work on the minimum sum of each depth. Next, print the statement “Total sum at each depth of non-cycle graph” and get the result.

Remember that, the queue of pairs is a container that contains the pairs of the element of the queue.

Example

In this program, we are going to calculate the sum of all minimum nodes at each depth.

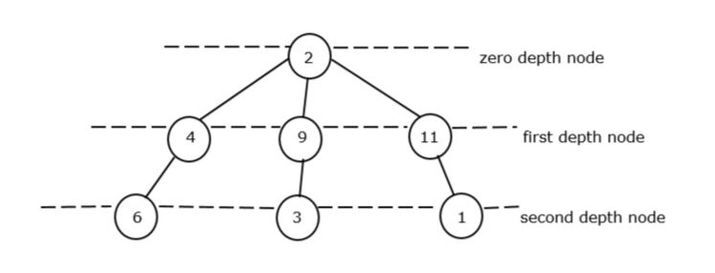
In this figure II, the minimum sum of total depth is 15+8+4+1 = 13.

Now we will take this figure as input to this program.

#include <iostream>
#include <queue> 

// required for FIFO operation
#include <utility> 

// required for queue pair
#include <climits>
using namespace std;

// create the structure definition for a binary tree node of non-cycle graph
struct tree_node {
   int val;
   tree_node *left;
   tree_node *right;
   tree_node(int x) {
      val = x;
      left = NULL;
      right = NULL;
   }
};
// This function is used to find the minimum sum at each depth
int minimum_sum_at_each_depth(tree_node* root) {
   if (root == NULL) {
      return 0;
   }
   queue<pair<tree_node*, int>> q;
   // create a queue to store node and depth and include pair to combine two together values.
   q.push(make_pair(root, 0)); 
   
   // construct a pair object with two element
   int present_depth = -1; 
   
   // present depth
   int present_sum = 0; 
   
   // present sum for present depth
   int totalSum = 0; 
   
   // Total sum for all depths
   while (!q.empty()) {
      pair<tree_node*, int> present = q.front(); 
      
      // assign queue pair - present
      q.pop();
      
      // delete an existing element from the beginning
      if (present.second != present_depth) {
      
         // We are moving to a new depth, so update the total sum and reset the present sum
         present_depth = present.second;
         totalSum += present_sum;
         present_sum = INT_MAX;
      }

      // Update the present sum with the value of the present node
      present_sum = min(present_sum, present.first->val);
      
      //We are adding left and right children to the queue for updating the new depth.
      if (present.first->left) {
         q.push(make_pair(present.first->left, present.second + 1));
      }
      if (present.first->right) {
         q.push(make_pair(present.first->right, present.second + 1));
      }
   }
   
   // We are adding the present sum of last depth to the total sum
   totalSum += present_sum;
   return totalSum;
}

// start the main function
int main() {
   tree_node *root = new tree_node(15);
   root->left = new tree_node(14);
   root->left->left = new tree_node(11);
   root->left->right = new tree_node(4);
   root->right = new tree_node(8);
   root->right->left = new tree_node(13);
   root->right->right = new tree_node(16);
   root->left->left->left = new tree_node(1);
   root->left->right->left = new tree_node(6);
   root->right->right->right = new tree_node(2);
   root->right->left->right = new tree_node(7);

   cout << "Total sum at each depth of non cycle graph: " << minimum_sum_at_each_depth(root) << endl; 
   return 0;
}

Output

Total sum at each depth of non cycle graph: 28

Conclusion

We explored the concept of the minimum sum of elements at each depth of a given non-cycle graph. We saw how the arrow operator connects the nodes and constructs the tree formation and using this it calculates the minimum sum at each depth. The application uses non cyclic graph such as city planning, network topologists, google map etc.