Check if a graph constructed from an array based on given conditions consists of a cycle or not

Introduction

In graph theory, it is a very important task to figure out if a graph built from an array and meeting certain conditions has a cycle or not. A graph is an imaginary way to show how things are linked together. It is used in a lot of places, like computer networks and social networks. This article talks about the conditions for graph construction, the BFS and DFS algorithm, and a step by step guide how loops in a undirected graph is identified.

Array Representation of a Graph

An array-based method in graph theory stores vertices and edges in arrays, which makes them easy to work with and use in algorithms. Starting with an empty graph and adding vertices and edges one at a time based on the information in the arrays is the foundation for further exploration, such as cycle detection, which is important for understanding how the graph is linked and if there are any loops.

Conditions for Graph Construction

Explanation of the given conditions

• The graph is constructed from an array, where the array represents a set of vertices and their connections or edges.

• Each element of the array corresponds to a vertex in the graph

• The value of each element in the array indicates the index of the vertex that it is connected to (its adjacent vertex).

• The array's index represents the vertex itself, and its corresponding value represents the vertex it is connected to.

Validating the conditions for graph construction

• Check if the array is valid and meets the required conditions before constructing the graph.

• Ensure that the array is not empty and contains at least one element to create a vertex.

• Verify that the array contains only non-negative integers since negative values or invalid data can't represent valid vertices or edges

• Ensure that the array indices are within the appropriate range. They should start from 0 to n-1, where n is the total number of vertices in the graph.

• Confirm that the values (connections) in the array are also within the valid range of 0 to n-1, ensuring they correspond to existing vertices

• Check for any duplicate connections or self-loops, as they violate the conditions for a valid graph

• Verify that there are no missing connections, meaning that all vertices are connected to form a complete graph or a connected component

DFS and BFS Algorithms

• Depth-First Search (DFS) is used for exploring a graph's vertices and edges by going as far as possible down each branch before turning around

Pseudo-code

procedure DFS(graph, start_vertex, visited)
   if start_vertex is not in visited:
      mark start_vertex as visited
      process start_vertex (e.g., check for cycles)
      for each neighbor in graph[start_vertex]:
      if neighbor is not in visited:
      DFS(graph, neighbor, visited)
   end if
end procedure
    pocedure DFS_Traversal(graph)
    visited = empty set
      for each vertex in graph:
      if vertex is not in visited:
         DFS(graph, vertex, visited)
   end for
end procedure

• Breadth-First Search (BFS) is a graph traversal algorithm that goes through all of a graph's vertices one level at a time. This makes it a great way to find cycles in graphs

Pseudo-code

procedure BFS(graph, start_vertex):
   create an empty queue Q
   create a set visited to keep track of visited vertices
   
   enqueue start_vertex into Q
   add start_vertex to visited set
   
   while Q is not empty:
      current_vertex = dequeue from Q
      for each neighbor_vertex of current_vertex:
         if neighbor_vertex is not in visited set:
            enqueue neighbor_vertex into Q
            add neighbor_vertex to visited set
      else:
         // A cycle is detected, return true
         return true
      // No cycle found, return false
      return false

Complexity

• Time complexity

Both BFS and DFS have a time complexity of O(V + E), where V is the number of vertices and E is the number of edges.

• Space Complexity

BFS and DFS have a time complexity of O(V).

Step-by-step cycle detection process

Let's consider a example with a graph

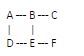
• Start with a set that is empty to monitor visited vertices

Visited set: {}

• Choose an arbitrary vertex as the beginning point for the cycle detection procedure. Let's choose vertex A.

Visited set: {A}
Current Vertex: A

• Examine the adjacent vertices of the current vertex (A). In this instance, A's neighbors are B and D. Add them to the visited set, and identify A as their parent node

Visited set: {A, B, D}
Current Vertex: A
Parent of B: A
Parent of D: A

• B is the next visited vertex in the visited set.

Visited set: {A, B, D}
Current Vertex: B
Parent of B: A

• Discover B's surroundings. B's immediate neighbors are A, C, and E. A is already in the set of visited vertices, but it is not the parent of B, so it does not constitute a cycle.

Visited set: {A, B, D, C, E}
Current Vertex: B

• Proceed to the next visited vertex, which is D.

Visited set: {A, B, D, C, E}
Current Vertex: D
Parent of D: A

• Discover D's acquaintances. A and E are D's closest neighbors. Since A is already included in the visited set and is the parent of D, there must be an edge (D -> A) connecting D to its parent. This indicates that the graph contains a cycle.

Cycle detected! There is an edge (D -> A) forming a cycle

The process ends here, and we have successfully detected the cycle in the graph using BFS i.e., (A->B->E->D->A).

Conclusion

In conclusion, it is important for many applications to be able to find cycles in a graph built from an array based on given parameters. This process helps find possible loops and solve real-world problems involving networks, circuits, and relationships, whether you use DFS or BFS. Cycle detection that works well improves the speed of algorithms and makes sure that data is correct.