Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Detect Cycle in a Directed Graph
Using a Depth First Search (DFS) traversal algorithm we can detect cycles in a directed graph. If there is any self-loop in any node, it will be considered as a cycle, otherwise, when the child node has another edge to connect its parent, it will also a cycle.
For the disconnected graph, there may different trees present, we can call them a forest. Now we have to detect cycle for all trees of the forest.
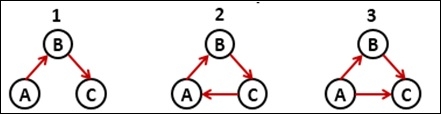
In this approach, we will use different sets to assign nodes to perform the DFS traversal. There are three different sets, the White, Grey and the Black. Initially, all nodes will be stored inside the white set. When one new node is traversed, it will be stored in the gray set and removed from the white one. And after completing backtracking, when that task for that node is completed, it will be swapped from gray to black set.
Input and Output
Input: The Adjacency matrix. 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 Output: The graph has cycle.
Algorithm
dfs(curr, wSet, gSet, bSet)
Input: Current node, the white, the grey and the black set.
Output: True if there is a cycle.
Begin delete curr from the while set and add it to the grey set for all nodes v connected with curr in the graph, do if v is in the black set, then skip next part, and go for next iteration if v is in the grey set, then return true if dfs(v, wSet, gSet, bSet) is true, then return true done delete curr from grey set and add to black set return fasle End
hasCycle(graph)
Input − Given Graph.
Output: True when the graph has cycled.
Begin initially insert all nodes into the white set while white set has some elements, do for all nodes v in the graph, do if v is not in the white set, then if dfs(v, wSet, gSet, bSet), then return true done done return false End
Example
#include<iostream>
#include<set>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 0, 0, 0},
{0, 0, 0, 0, 0},
{1, 0, 0, 1, 0},
{0, 0, 0, 0, 1},
{0, 0, 1, 0, 0}
};
bool dfs(int curr, set<int>&wSet, set<int>&gSet, set<int>&bSet) {
//moving curr to white set to grey set.
wSet.erase(wSet.find(curr));
gSet.insert(curr);
for(int v = 0; v < NODE; v++) {
if(graph[curr][v] != 0) { //for all neighbour vertices
if(bSet.find(v) != bSet.end())
continue; //if the vertices are in the black set
if(gSet.find(v) != gSet.end())
return true; //it is a cycle
if(dfs(v, wSet, gSet, bSet))
return true; //cycle found
}
}
//moving v to grey set to black set.
gSet.erase(gSet.find(curr));
bSet.insert(curr);
return false;
}
bool hasCycle() {
set<int> wSet, gSet, bSet; //three set as white, grey and black
for(int i = 0; i<NODE; i++)
wSet.insert(i); //initially add all node into the white set
while(wSet.size() > 0) {
for(int current = 0; current < NODE; current++) {
if(wSet.find(current) != wSet.end())
if(dfs(current, wSet, gSet, bSet))
return true;
}
}
return false;
}
int main() {
bool res;
res = hasCycle();
if(res)
cout << "The graph has cycle." << endl;
else
cout << "The graph has no cycle." << endl;
}Output
The graph has cycle.
2K+ Views
