Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Succinct Encoding of Binary Tree in C++
Suppose we have a binary tree. As we know the succinct encoding of Binary Tree performs close to lowest possible space. The n’th Catalan number is designated by the number of structurally different binary trees with n different nodes. If the n is large, this is about 4n; thus, we require minimum about log2(4) n = 2n bits to encode it. A succinct binary tree therefore would consume 2n + O(n) bits.
So, if the input is like
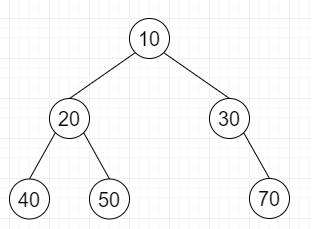
then the output will be
encoded −
Structure List 1 1 1 0 0 1 0 0 1 0 1 0 0
Data List 10 20 40 50 30 70
Decoded − The tree as shown above.
To solve this, we will follow these steps −
- Define a function Encode(), this will take root, a list named struc, a list named data,
- if root is same as NULL, then −
- insert 0 at the end of struc
- return
- insert 1 at the end of struc
- insert value of root at the end of data
- Encode(left of root, struc, data)
- Encode(right of root, struc, data)
- Define a function Decode(), this will take a list named struc, a list named data,
- if size of struc <= 0, then −
- return NULL
- vb := first element of struc
- delete front element from struc
- if b is same as 1, then −
- key := first element of data
- delete front element from data
- root = new node with key
- left of root := Decode(struc, data)
- right of root := Decode(struc, data)
- return root
- return NULL
Example (C++)
Let us see the following implementation to get better understanding −
#include<bits/stdc++.h>
using namespace std;
class TreeNode {
public:
int val;
TreeNode *left, *right;
TreeNode(int data) {
val = data;
left = NULL;
right = NULL;
}
};
void Encode(TreeNode *root, list<bool>&struc, list<int>&data){
if(root == NULL){
struc.push_back(0);
return;
}
struc.push_back(1);
data.push_back(root->val);
Encode(root->left, struc, data);
Encode(root->right, struc, data);
}
TreeNode *Decode(list<bool>&struc, list<int>&data){
if(struc.size() <= 0)
return NULL;
bool b = struc.front();
struc.pop_front();
if(b == 1){
int key = data.front();
data.pop_front();
TreeNode *root = new TreeNode(key);
root->left = Decode(struc, data);
root->right = Decode(struc, data);
return root;
}
return NULL;
}
void preorder_trav(TreeNode* root){
if(root){
cout << "key: "<< root->val;
if(root->left)
cout << " | left child: "<< root->left->val;
if(root->right)
cout << " | right child: "<< root->right->val;
cout << endl;
preorder_trav(root->left);
preorder_trav(root->right);
}
}
main() {
TreeNode *root = new TreeNode(10);
root->left = new TreeNode(20);
root->right = new TreeNode(30);
root->left->left = new TreeNode(40);
root->left->right = new TreeNode(50);
root->right->right = new TreeNode(70);
cout << "The Tree\n";
preorder_trav(root);
list<bool> struc;
list<int> data;
Encode(root, struc, data);
cout << "\nEncoded Tree\n";
cout << "Structure List\n";
list<bool>::iterator si; // Structure iterator
for(si = struc.begin(); si != struc.end(); ++si)
cout << *si << " ";
cout << "\nData List\n";
list<int>::iterator di; // Data iIterator
for(di = data.begin(); di != data.end(); ++di)
cout << *di << " ";
TreeNode *newroot = Decode(struc, data);
cout << "\n\nPreorder traversal of decoded tree\n";
preorder_trav(newroot);
}Input
root->left = new TreeNode(20); root->right = new TreeNode(30); root->left->left = new TreeNode(40); root->left->right = new TreeNode(50); root->right->right = new TreeNode(70);
Output
The Tree key: 10 | left child: 20 | right child: 30 key: 20 | left child: 40 | right child: 50 key: 40 key: 50 key: 30 | right child: 70 key: 70 Encoded Tree Structure List 1 1 1 0 0 1 0 0 1 0 1 0 0 Data List 10 20 40 50 30 70 Preorder traversal of decoded tree key: 10 | left child: 20 | right child: 30 key: 20 | left child: 40 | right child: 50 key: 40 key: 50 key: 30 | right child: 70 key: 70
Updated on: 27-Aug-2020
245 Views
Advertisements