Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Boundary of Binary Tree in C++
Suppose we have a binary tree, we have to find the values of its boundary in anti-clockwise direction starting from root. Here boundary includes left boundary, leaves, and the right boundary in order without duplicate nodes.
The left boundary is the path from root to the left-most node.
The Right boundary is the path from root to the right-most node.
When the root doesn't have left subtree or right subtree, then the root itself is left boundary or right boundary.
So, if the input is like
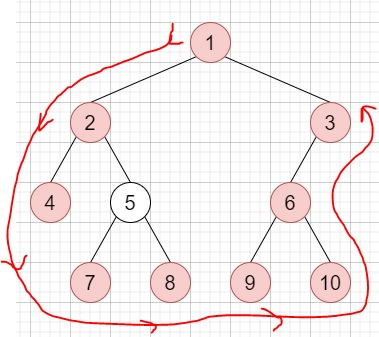
then the output will be [1,2,4,7,8,9,10,6,3]
To solve this, we will follow these steps −
Define an array ret
Define a function leftBoundary(), this will take node,
if node is null or node is leaf, then −
return
insert value of node into ret
if left of node is present, then −
leftBoundary(left of node)
Otherwise
leftBoundary(right of node)
Define a function rightBoundary(), this will take node,
if node is null or node is leaf, then −
return
insert value of node into ret
if right of node is present, then −
rightBoundary(left of node)
Otherwise
rightBoundary(right of node)
Define a function leaves(), this will take node,
if node is not present, then −
return
if node is leaf, then −
insert val of node into ret
leaves(left of node)
leaves(right of node)
From the main method do the following −
Clear the ret array
if root is not present, then −
return ret
insert val of root into ret
leftBoundary(left of root)
leaves(left of root);
leaves(right of root);
rightBoundary(right of root)
return ret
Example
Let us see the following implementation to get a better understanding −
#include <bits/stdc++.h>
using namespace std;
void print_vector(vector<auto> v){
cout << "[";
for(int i = 0; i<v.size(); i++){
cout << v[i] << ", ";
}
cout << "]"<<endl;
}
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
}else{
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
}else{
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int> v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
class Solution {
public:
vector<int> ret;
void leftBoundary(TreeNode* node){
if (!node || node->val == 0 || (!node->left && !node->right))
return;
ret.push_back(node->val);
if (node->left && node->left->val != 0)
leftBoundary(node->left);
else
leftBoundary(node->right);
}
void rightBoundary(TreeNode* node){
if (!node || node->val == 0 || (!node->left && !node->right))
return;
if (node->right && node->right->val != 0) {
rightBoundary(node->right);
}
else {
rightBoundary(node->left);
}
ret.push_back(node->val);
}
void leaves(TreeNode* node){
if (!node || node->val == 0)
return;
if (!node->left && !node->right) {
ret.push_back(node->val);
}
leaves(node->left);
leaves(node->right);
}
vector<int> boundaryOfBinaryTree(TreeNode* root){
ret.clear();
if (!root)
return ret;
ret.push_back(root->val);
leftBoundary(root->left);
leaves(root->left);
leaves(root->right);
rightBoundary(root->right);
return ret;
}
};
main(){
Solution ob;
vector<int> v = {1,2,3,4,5,6,NULL,NULL,NULL,7,8,9,10};
TreeNode *root = make_tree(v);
print_vector(ob.boundaryOfBinaryTree(root));
}Input
{1,2,3,4,5,6,NULL,NULL,NULL,7,8,9,10}Output
[1, 2, 4, 7, 8, 9, 10, 6, 3, ]
136 Views
