Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Tree Cameras in C++
Suppose we have a binary tree; we place cameras on the nodes of the tree. Now each camera at a node can monitor its parent, itself, and its children. We have to find the minimum number of cameras needed to monitor all nodes of the tree.
So, if the input is like −
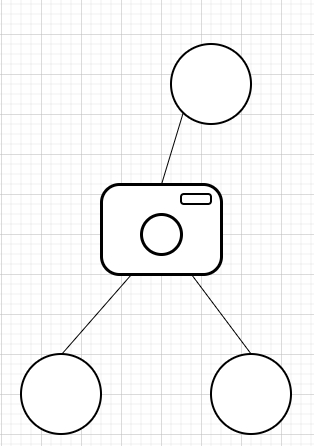
then the output will be 1, because only one camera is enough to track all.
To solve this, we will follow these steps −
Define one set called covered, of type TreeNode (Tree node has left, right and data field)
Define a function solve(), this will take node, parent,
if node is null, then −
return
solve(left of node, node)
solve(right of node, node)
if (parent is same as NULL and (node, left of node, right of node) nothing is covered, then −
(increase ans by 1)
insert node into covered
insert left of node into covered
insert right of node into covered
insert parent into covered
From the main method do the following,
ans := 0
insert NULL into covered
solve(root, NULL)
return ans
Let us see the following implementation to get better understanding −
Example
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
class Solution {
public:
set<TreeNode*> covered;
int ans;
int minCameraCover(TreeNode* root){
covered.clear();
ans = 0;
covered.insert(NULL);
solve(root, NULL);
return ans;
}
void solve(TreeNode* node, TreeNode* parent){
if (!node)
return;
solve(node->left, node);
solve(node->right, node);
if ((parent == NULL && covered.find(node) == covered.end())
|| covered.find(node->left) == covered.end() || covered.find(node-
>right) == covered.end()) {
ans++;
covered.insert(node);
covered.insert(node->left);
covered.insert(node->right);
covered.insert(parent);
}
}
};
main(){
Solution ob;
TreeNode *root = new TreeNode(1);
root->left = new TreeNode(1);
root->left->left = new TreeNode(1); root->left->right = new
TreeNode(1);
cout << (ob.minCameraCover(root));
}Input
[1,1,NULL,1,1]
Output
1
170 Views
