Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Statically and Dynamically Induced EMF
Induced EMF
When a magnetic flux linking a conductor or coil changes, an electromotive force (EMF) is induced in the conductor or coil, is known as induced EMF. Depending upon the way of bringing the change in magnetic flux, the induced EMF is of two types −
- Statically Induced EMF
- Dynamically Induced EMF
Statically Induced EMF
When the conductor is stationary and the magnetic field is changing, the induced EMF in such a way is known as statically induced EMF (as in a transformer). It is so called because the EMF is induced in a conductor which is stationary. The statically induced EMF can also be classified into two categories −
- Statically Induced EMF
- Mutually Induced EMF
Self-Induced EMF
When an EMF is induced in the coil due to the change of its own magnetic flux linked with it is known as self-induced EMF.
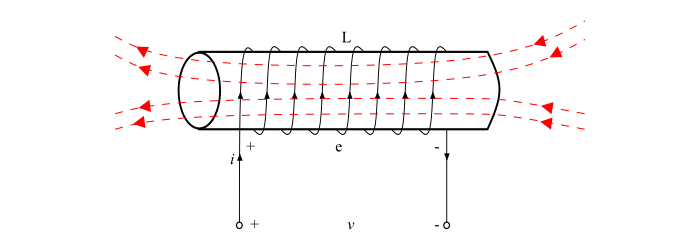
Explanation − When a current flows in a coil, a magnetic field produced by this current through the coil. If the current in the coil changes, then the magnetic field linking the coil also changes. Therefore, according to Faraday’s law of electromagnetic induction, an EMF being induced in the coil. The induced EMF in such a way is known as self-induced EMF.
Mathematically, self-induced EMF is given by,
$$\mathrm{e=L\frac{di}{dt}\:\:\:\:\:\:...(1)}$$
Where, L is the self-inductance of the coil.
Mutually Induced EMF
When an EMF is induced in a coil due to changing magnetic flux of neighbouring coil is known as mutually induced EMF.
Explanation − Consider two coils coil-1 and coil-2 placed adjacent to each other (see the figure). A fraction of the magnetic flux produced by coil-1 links with the coil-2. This magnetic flux which is common to both the coils 1 and 2 is known as mutual flux $(\varphi_{m})$. Now, if the current in coil-1 changes, the mutual flux also changes and thus EMF being induced in both the coils. The EMF induced in coil-2 is known as mutually induced EMF, since it is induced due changing in flux which is produced by coil-1. Mathematically, the mutually induced EMF is given by,
$$\mathrm{e_{m}=M\frac{di_{1}}{dt}\:\:\:\:\:\:...(2)}$$
Where, M is the mutual inductance between the coils.
Dynamically Induced EMF
When the conductor is moved in a stationary magnetic field so that the magnetic flux linking with it changes in magnitude, as the conductor is subjected to a changing magnetic, therefore an EMF will be induced in it. The EMF induced in this way is known as dynamically induced EMF (as in a DC or AC generator). It is so called because EMF is induced in a conductor which is moving (dynamic).
Explanation − Consider a conductor of length l meters moving with a velocity of v m/s at right angles to a uniform stationary magnetic field of flux density B Wb/m2.Let the conductor moves through a small distance dx in time dt seconds. Then,
$$\mathrm{Area\: swept\: by \:conductor,\mathit{a = l \times dx}\: \:m^{2}}$$
$$\mathrm{\therefore Magnetic\: flux\: cut\: by\: conductor,\mathit{dψ}= Magnetic \:Flux \:Density \:\times\: Area \:Swept}$$
$$\mathrm{\Longrightarrow \mathit{dψ=B \:l\:dx}\: \:Wb}$$
Now, according to Faraday’s law of electromagnetic induction, the induced EMF will be,
$$\mathrm{\mathit{e=N\frac{dψ}{dt}=\frac{B\:l\:dx}{dt}\: (\because N}=1)}$$
$$\mathrm{\because \mathit{\frac{dx}{dt}}=Velocity \mathit{V}}$$
$$\mathrm{\therefore \mathit{e=B\: l\:v}\: \:Volts\:\:\:\:\:\:...(3)}$$
Equation (3) gives the dynamically induced EMF when the conductor moves at right angle to the magnetic field.
If the conductor moves at an angle &theta to the magnetic field, then the EMF induced due to only the perpendicular component of the velocity to the magnetic field.
$$\mathrm{\mathit{e=B\:l\:v} \:sinθ\:\:\:\:\:\:...(4)}$$
Numerical Example
A conductor of length of 0.8 m lies in and at right angle to a uniform magnetic field of flux density 2 $Wb/m^{2}$. The conductor moves with a velocity of 30 m/s. Calculate the EMF induced in the conductor. What will be the EMF induced if the conductor moves at an angle of 45° to the magnetic field?
Solution
Case 1 − When conductor moves at right angle to the magnetic field.
$$\mathrm{\mathit{e=B\:l\:v}=2\times(0.8)\times(30)=48V}$$
Case 2 − When the conductor moves at 45° to the magnetic field.
$$\mathrm{\mathit{e=B\:l\:v}\:sinθ=2\times(0.8)\times(30)\times sin45=33.95V}$$
19K+ Views
