Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Source Transformation with Solved Examples
A practical voltage source consists of an ideal voltage source in series with an internal resistance (for an ideal voltage source, this internal resistance being zero, so that the output voltage becomes independent of the load current) While a practical current source consists of an ideal current source in parallel with an internal resistance (for an ideal current source, this parallel resistance is infinity).
The practical voltage and current sources are mutually transferable i.e. a practical voltage source can be converted into a practical current source and vice-versa.
Voltage to Current Source Transformation
Consider a practical voltage of V volts having a series internal resistance Rint ohms. A load resistance of RL ohms is connected across the load terminals.
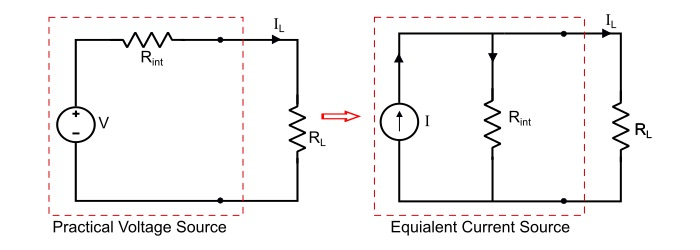
Therefore, by referring the circuit of practical voltage source, the load current is
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}}{\mathit{R}_{int}+ \mathit{R}_{L}}=\frac{\mathit{V} \mathit{R}_{int}}{(\mathit{R}_{int}+\mathit{R}_{L})\mathit{R}_{int}}=\frac{\mathit{V}}{\mathit{R}_{int}}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}\:\:\:…(1)$$
Now, refer the equivalent circuit of current source, the load current is
$$\mathrm{\mathit{I}_{L}=\mathit{I}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+ \mathit{R}_{L}})}\:\:\:…(2)$$
Two sources to become identical, the equation (1) and (2) should produce the same result i.e.
$$\mathrm{\frac{\mathit{V}}{\mathit{R}_{int}}(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+ \mathit{R}_{L}})=\mathit{I}(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+ \mathit{R}_{L}})}$$
$$\mathrm{\Rightarrow\:\mathit{I}=\frac{\mathit{V}}{\mathit{R}_{int}}}\:\:\:…(3)$$
Thus, a practical voltage source of constant voltage V and internal resistance Rint is equivalent to a current source of current I = V/Rint and internal resistance Rint in parallel with current source.
Here, the internal resistance of the equivalent current source has the same value as the internal resistance of the voltage source.
Current to Voltage Source Transformation
Consider a practical current source of constant current I amperes with a parallel internal resistance Rint, it can be converted into an equivalent voltage source as follows.
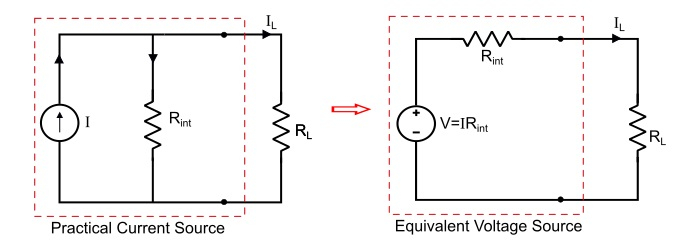
Refer the circuit of current source, the load current is
$$\mathrm{\mathit{I}_{L}=\mathit{I}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}\:\:\:… (4)$$
Refer the equivalent circuit of voltage source, the load current is
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}}{\mathit{R}_{int}+\mathit{R}_{L}}=\frac{V/\mathit{R}_{int}}{(\mathit{R}_{int}+\mathit{R}_{L})/\mathit{R}_{int}}=\frac{V}{\mathit{R}_{int}}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}\:\:\:…(5)$$
For the two sources to become identical,
$$\mathrm{\frac{\mathit{V}}{\mathit{R}_{int}}(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})=I(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}$$
$$\mathrm{\Rightarrow\:\mathit{i}=\frac{\mathit{v}}{\mathit{R}_{int}}}$$
$$\mathrm{\Rightarrow\:\mathit{v}=\mathit{I}{\mathit{R}_{int}}}\:\:\:… (6)$$
Therefore, a current source can be converted into an equivalent voltage source, where the value of voltage of the equivalent voltage source is V = IRint and the series resistance Rint of voltage source has the same value as the parallel resistance of the current source.
Numerical Example - 1
Convert a voltage source of 24 V having a series internal resistance of 2 Ω into an equivalent current source.
Solution
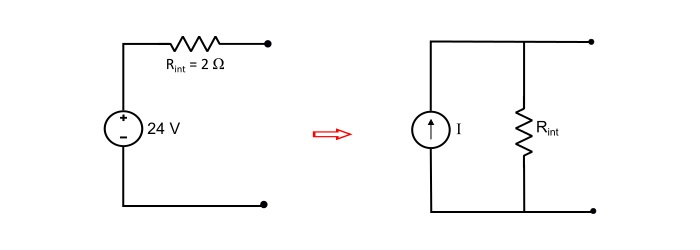
Here, the source current of equivalent current source is
$$\mathrm{\mathit{I}=\frac{\mathit{V}}{\mathit{R}_{int}}=\frac{24}{2}=12\:A}$$
The internal resistance Rint of the equivalent current source has the same value as the original voltage source, thus
$$\mathrm{\mathit{R}_{int}=2\:Ω}$$
Numerical Example - 2
A battery has an internal resistance of 2 Ω and open circuit voltage of 24 V. What is the power lost within the battery and terminal voltage when a load resistance of 6 Ω is connected across the terminals of the battery?
Solution
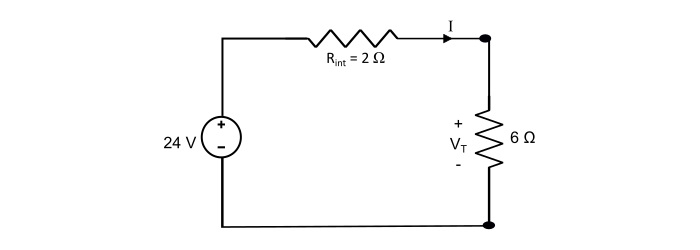
The total circuit current is
$$\mathrm{\mathit{I}=\frac{24}{2+6}=3\:A}$$
$$\mathrm{Power\:lost\:within\:battery=\mathit{I}^{2}\mathit{R}_{int}=3^{2}×2=18\:W}$$
$$\mathrm{Terminal\:Votage\:(\mathit{V}_{r})=\mathit{IR}_{L}=3×6=18\:V}$$
17K+ Views
