Seaborn - Linear Relationships

---

---

Most of the times, we use datasets that contain multiple quantitative variables, and the goal of an analysis is often to relate those variables to each other. This can be done through the regression lines.

While building the regression models, we often check for multicollinearity, where we had to see the correlation between all the combinations of continuous variables and will take necessary action to remove multicollinearity if exists. In such cases, the following techniques helps.

Functions to Draw Linear Regression Models

There are two main functions in Seaborn to visualize a linear relationship determined through regression. These functions are regplot() and lmplot().

regplot vs lmplot

Let us now draw the plots.

Example

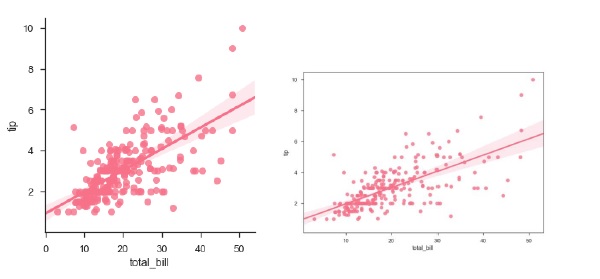
Plotting the regplot and then lmplot with the same data in this example

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('tips')
sb.regplot(x = "total_bill", y = "tip", data = df)
sb.lmplot(x = "total_bill", y = "tip", data = df)
plt.show()

Output

You can see the difference in the size between two plots.

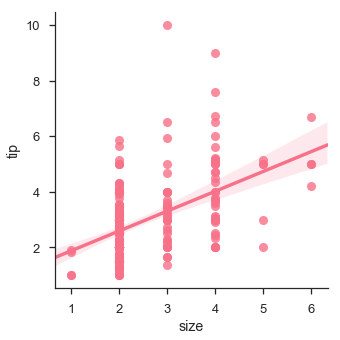
We can also fit a linear regression when one of the variables takes discrete values

Example

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('tips')
sb.lmplot(x = "size", y = "tip", data = df)
plt.show()

Output

Fitting Different Kinds of Models

The simple linear regression model used above is very simple to fit, but in most of the cases, the data is non-linear and the above methods cannot generalize the regression line.

Let us use Anscombe’s dataset with the regression plots −

Example

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
sb.lmplot(x="x", y="y", data=df.query("dataset == 'I'"))
plt.show()

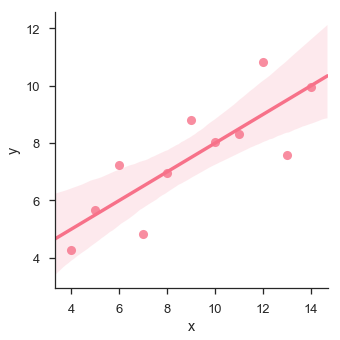
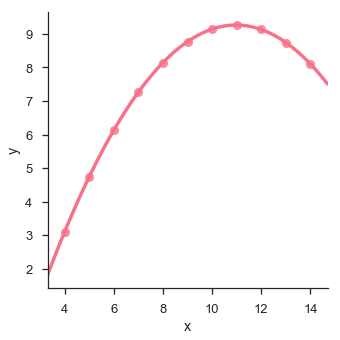
In this case, the data is good fit for linear regression model with less variance.

Let us see another example where the data takes high deviation which shows the line of best fit is not good.

Example

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
sb.lmplot(x = "x", y = "y", data = df.query("dataset == 'II'"))
plt.show()

Output

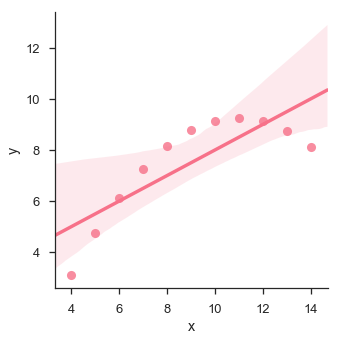
The plot shows the high deviation of data points from the regression line. Such non-linear, higher order can be visualized using the lmplot() and regplot().These can fit a polynomial regression model to explore simple kinds of nonlinear trends in the dataset −

Example

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
sb.lmplot(x = "x", y = "y", data = df.query("dataset == 'II'"),order = 2)
plt.show()

Output