Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Rotating Magnetic Field Produced by Two-Phase Supply
A 1-phase supply produces a pulsating magnetic field which does not rotate in the space. Therefore, a 1-phase supply cannot produce rotation in a stationary rotor. Although, like a 3-phase supply, the 2-phase supply can also produce a rotating magnetic field of constant magnitude. Therefore, all the single-phase induction motors, except shaded pole induction motor, are started as 2-phase motor. Once so started, the motor will continue to run on the 1-phase supply.
How does a 2-Phase Supply Produce Rotating Magnetic Field of Constant Magnitude?
Consider a 2-phase, 2 pole motor, where the phases A and B are fed by a balanced 2-phase supply and the currents in these phases are IA and IB respectively as shown in the figure.
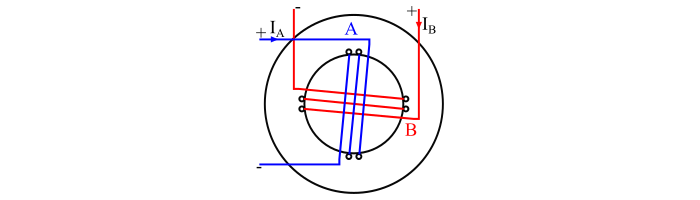
It is clear that the current IA leads the current IB by angle of 90°. Therefore, the fluxes produced by these currents can be written as,
$$\mathrm{φ_{π΄} = φ_{π}\:sin(\omega π‘ + 90°) = φ_{π}\:cos\:\omega π‘ … (1)}$$
$$\mathrm{φ_{π΅} = φ_{π}\:sin\:\omega π‘ … (2)}$$
Where, φm is the maximum value of the flux produced by the current in either phase.
We shall now prove that this two-phase supply produces a magnetic flux of constant magnitude which rotates in the space.
At Instant-1
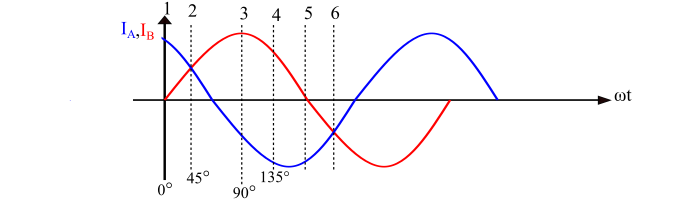
Refer the waveform of the currents IA and IB. Here, at the instant-1, the current is zero in phase B and positive maximum in the phase A. Also, the instant 1 corresponds to ωt = 0°, hence, the fluxes are given by,
$$\mathrm{φ_{π΄} = φ_{m}\:cos\:\omega π‘ = φ_{m}\:cos\:0 = φ_{m}}$$
And
$$\mathrm{φ_{π΅} = φ_{m}\:sin\:\omega π‘ = φ_{m}\:sin\:0 = 0}$$
Therefore, the resultant flux at instant 1 is
$$\mathrm{φ_{π } = \sqrt{{φ^{2}_{π΄}}+{φ^{2}_{B}}}=\sqrt{(φ_{π})^{2}+(0)^{2}}= φ_{π}}$$
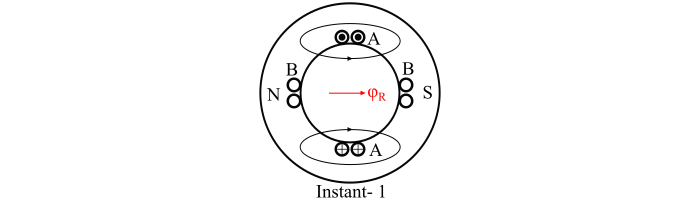
Hence, the magnitude of resultant flux is equal to φm and is directed towards right as shown in the figure instant-1
At Instant-2
At this instant, the current in the phase A is still flowing in the same direction and an equal current is flowing in the phase B. This instant corresponds to ωt = 45°, so that,
$$\mathrm{φ_{π΄} = φ_{m}\:cos\:\omega π‘ = φ_{m}\:cos\:45 =\frac{1}{\sqrt{2}}φ_{m}}$$
And
$$\mathrm{π_{π΅} = π_{π}\:sin\:\omega π‘ = π_{π} \:sin\:45 =\frac{1}{\sqrt{2}}φ_{m}}$$
Therefore, the resultant flux is given by,
$$\mathrm{π_{π } =\sqrt{{φ^{2}_{π΄}}+{φ^{2}_{B}}}=\sqrt{(\frac{φ_{m}}{\sqrt{2}})^{2}+(\frac{φ_{m}}{\sqrt{2}})^{2}}=φ_{m}}$$
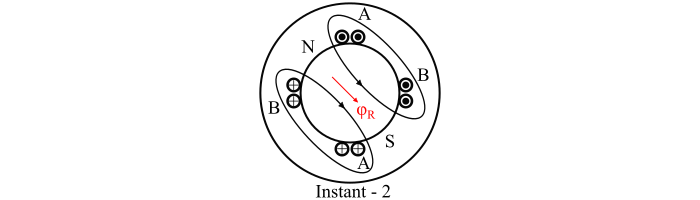
Hence, the resultant flux has same value but turned by an angle of 45° in the clockwise direction from Instant-1 (see the figure of Instant-2).
At Instant-3
At Instant-3, the current in the phase A has reduced to 0 and the current in phase B has increased to the positive maximum value. This instant is corresponds to ωt = 90° in the waveform diagram, so that,
$$\mathrm{φ_{π΄} = φ_{m}\:cos\:ωt = φ_{m}\:cos\:90 = 0}$$
And
$$\mathrm{π_{π΅} = φ_{m}\:sin\:ωt = φ_{m}\:sin\:90 = φ_{m}}$$
Therefore, the resultant flux is given by,
$$\mathrm{π_{π } =\sqrt{{φ^{2}_{π΄}}+{φ^{2}_{B}}}=\sqrt{({0})^{2}+({φ_{m}})^{2}}=φ_{m}}$$
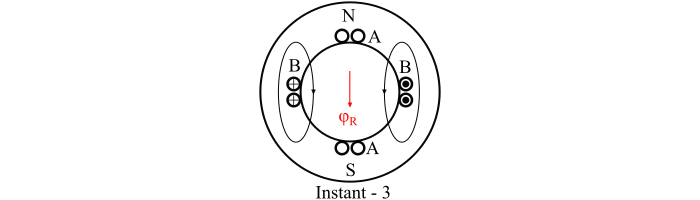
Hence, again the resultant flux has the same magnitude equal to φm, but has turned by an angle of 90° in the clockwise direction from the instant 1 (see the figure of Instant-3).
At Instant-4
At Instant-4, the current in phase A is reversed and has the same value as that in the phase B (the current IB is positive). This instant corresponds to ωt = 135°, hence the flux is given by,
$$\mathrm{π_{π΄} = π_{π}\:cos\:ωt = π_{π} \:cos\:135 =-\frac{1}{\sqrt{2}}π_{π}}$$
And
$$\mathrm{π_{π΅} = π_{π}\:cos\:ωt = π_{π} \:cos\:135 =\frac{1}{\sqrt{2}}π_{π}}$$
Therefore, the resultant flux is given by,
$$\mathrm{π_{π } =\sqrt{{φ^{2}_{π΄}}+{φ^{2}_{B}}}=\sqrt{(-\frac{φ_{m}}{\sqrt{2}})^{2}+(\frac{φ_{m}}{\sqrt{2}})^{2}}=φ_{m}}$$
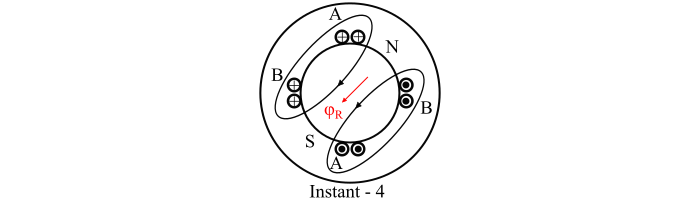
Again, the resultant flux has the same magnitude, but has turned by an angle of 135° from Instant-1 as shown in the figure of Instant-4. We shall continue to consider other instants to this fact.
From the above discussion, it is clear that a balanced 2-phase supply produces a rotating magnetic field of constant value equal to φm. The speed of the rotation of the magnetic field is called as the synchronous speed and is given by,
$$\mathrm{π_{π} =\frac{120π}{π}}$$
Where,
- P is the number poles in the machine, and
- f is the supply frequency.
1K+ Views
