Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Magnetic Field Intensity of an Electromagnet
The magnetic field intensity is the force acting on a unit test north-pole (i.e., N-pole of 1 Wb) placed at a point in the magnetic field. It is denoted by H.
The magnetic field intensity is a vector quantity, possessing both magnitude and direction.
The magnetic field intensity is also known by different names like Magnetising Force, Magnetic Field Strength, and Magnetic Potential Gradient etc.
Explanation
Consider a point x situated at a distance r meters from a pole of m Wb. Let a unit north-pole (i.e., a pole of 1 Wb) is placed at point x.
Hence, by the definition, the magnetic field intensity at point x is the force acting on the unit north-pole placed at point x, i.e.,
Magnetic field intensity at 𝑥, 𝐻 = Force on unit north − pole at 𝑥
Therefore, according to Coulomb’s law of magnetism,
$$\mathrm{H=\frac{1}{4\pi\:\mu_{0}\mu_{r}}(\frac{m_{1}m_{2}}{r^{2}})=\frac{1}{4\pi\:\mu_{0}}(\frac{m\times\:1}{r^{2}})\:\:\:\:\:(\because\:\mu_{r(air)}=1)}$$
$$\mathrm{\Rightarrow\:H=\frac{1}{4\pi\:\mu_{0}}(\frac{m}{r^{2}})\:\:\:...(1)}$$
Thus, the eq. (1) gives the magnetic field intensity at point x placed in the magnetic flied of a magnetic pole of strength of m Wb.
Unit of Magnetic Field Intensity
Since, by the definition of magnetic field intensity, we can write,
$$\mathrm{H=Force\:on\:a\:magnetic\:pole=\frac{Force(F)}{Pole\:strength (𝑚)=\frac{Newton}{Weber}}=N/Wb}$$
Therefore, the magnetic field intensity is measured in Newton per Weber (N/Wb).
Magnetic Field Intensity of an Electromagnet
An electromagnetic is coil wound on a core of magnetic material.
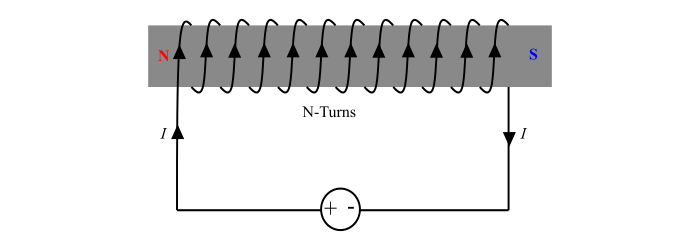
Consider a coil of N turns, a current of I amperes flowing through it, then
Magnetic field intensity,
$$\mathrm{H=\frac{NI}{l}\:\:AT/m\:\:\:...(2)}$$
Where,
NI is called as mmf,
l is the length of magnetic circuit in m.
The eq. (2) defines AT/m as the unit of magnetic field intensity, that equivalent to N/Wb.
Important – The magnetic field intensity can also be given in terms of magnetic flux density (B) as follows,
$$\mathrm{B=\mu_{0}\mu_{r}H}$$
$$\mathrm{\Rightarrow\:H=\frac{B}{\mu_{0}\mu_{r}}\:\:\:...(3)}$$
Numerical Example (1)
A magnetic field is produces by a pole of strength 100 mWb placed in vacuum. Determine the magnetic field intensity at point x in the magnetic field at a distance of 2 meters from the pole.
Solution −
Since, the pole is placed in vacuum, thus the magnetic field intensity will be,
$$\mathrm{H=\frac{1}{4\pi\:\mu_{0}}(\frac{m}{r^{2}})=\frac{1}{4\pi\:(4\pi\times\:10^{-7})}(\frac{100\times\:10^{-3}}{2^{2}})}$$
$$\mathrm{\Rightarrow\:H=1.584\times\:10^{3}\:N/Wb}$$
Numerical Example (2)
A toroidal coil has a magnetic path length of 40 cm and the number of turns in the coil is 600. The coil current is 200 mA. Calculate the intensity of magnetic field produced by the coil.
Solution −
For a coil, the magnetic field intensity is given by,
$$\mathrm{H=\frac{NI}{l}=\frac{600\times\:200\times\:10^{-3}}{40\times\:10^{-2}}=300\:AT/m}$$
Numerical Example (3)
Determine the magnetic field intensity, when the magnetic flux density in an air gap is equal to 0.05 T.
Solution −
Here, Magnetic field intensity in air gap,
$$\mathrm{H=\frac{B}{\mu_{0}}=\frac{0.05}{4\pi\:\times10^{-7}}=3.981\times\:10^{4}\:AT/m}$$
2K+ Views
