
- Python - Home
- Python - Overview
- Python - History
- Python - Features
- Python vs C++
- Python - Hello World Program
- Python - Application Areas
- Python - Interpreter
- Python - Environment Setup
- Python - Virtual Environment
- Python - Basic Syntax
- Python - Variables
- Python - Private Variables
- Python - Data Types
- Python - Type Casting
- Python - Unicode System
- Python - Literals
- Python - Operators
- Python - Arithmetic Operators
- Python - Comparison Operators
- Python - Assignment Operators
- Python - Logical Operators
- Python - Bitwise Operators
- Python - Membership Operators
- Python - Identity Operators
- Python - Walrus Operator
- Python - Operator Precedence
- Python - Comments
- Python - User Input
- Python - Numbers
- Python - Booleans
- Python - Floating Points
- Python - Control Flow
- Python - Decision Making
- Python - If Statement
- Python - If else
- Python - Nested If
- Python - Conditional User Inputs
- Python - Match-Case Statement
- Python - Loops
- Python - for Loops
- Python - for-else Loops
- Python - While Loops
- Python - break Statement
- Python - continue Statement
- Python - pass Statement
- Python - Nested Loops
- Python Functions & Modules
- Python - Functions
- Python - Default Arguments
- Python - Keyword Arguments
- Python - Keyword-Only Arguments
- Python - Positional Arguments
- Python - Positional-Only Arguments
- Python - Arbitrary Arguments
- Python - Variables Scope
- Python - Function Annotations
- Python - Modules
- Python - Packing and Unpacking
- Python - Built in Functions
- Python Strings
- Python - Strings
- Python - Slicing Strings
- Python - Modify Strings
- Python - String Concatenation
- Python - String Formatting
- Python - Escape Characters
- Python - String Methods
- Python - String Exercises
- Python Lists
- Python - Lists
- Python - Access List Items
- Python - Change List Items
- Python - Add List Items
- Python - Remove List Items
- Python - Loop Lists
- Python - List Comprehension
- Python - Sort Lists
- Python - Copy Lists
- Python - Join Lists
- Python - List Methods
- Python - List Exercises
- Python Tuples
- Python - Tuples
- Python - Access Tuple Items
- Python - Update Tuples
- Python - Unpack Tuples
- Python - Loop Tuples
- Python - Join Tuples
- Python - Tuple Methods
- Python - Namedtuple
- Python - Tuple Exercises
- Python Sets
- Python - Sets
- Python - Access Set Items
- Python - Add Set Items
- Python - Remove Set Items
- Python - Loop Sets
- Python - Join Sets
- Python - Copy Sets
- Python - Set Operators
- Python - Set Methods
- Python - Set Exercises
- Python Dictionaries
- Python - Dictionaries
- Python - Access Dictionary Items
- Python - Change Dictionary Items
- Python - Add Dictionary Items
- Python - Remove Dictionary Items
- Python - Dictionary View Objects
- Python - Loop Dictionaries
- Python - Copy Dictionaries
- Python - Nested Dictionaries
- Python - Dictionary Methods
- Python - Dictionary Exercises
- Python Arrays
- Python - Arrays
- Python - Access Array Items
- Python - Add Array Items
- Python - Remove Array Items
- Python - Loop Arrays
- Python - Copy Arrays
- Python - Reverse Arrays
- Python - Sort Arrays
- Python - Join Arrays
- Python - Array Methods
- Python - Array Exercises
- Python File Handling
- Python - File Handling
- Python - Write to File
- Python - Read Files
- Python - Renaming and Deleting Files
- Python - Directories
- Python - File Methods
- Python - OS File/Directory Methods
- Python - OS Path Methods
- Object Oriented Programming
- Python - OOPs Concepts
- Python - Classes & Objects
- Python - Class Attributes
- Python - Class Methods
- Python - Static Methods
- Python - Constructors
- Python - Access Modifiers
- Python - Inheritance
- Python - Multiple Inheritance
- Python - Multilevel Inheritance
- Python - Polymorphism
- Python - Method Overriding
- Python - Method Overloading
- Python - Dynamic Binding
- Python - Dynamic Typing
- Python - Abstraction
- Python - Encapsulation
- Python - Interfaces
- Python - Packages
- Python - Inner Classes
- Python - Anonymous Class and Objects
- Python - Singleton Class
- Python - Wrapper Classes
- Python - Enums
- Python - Reflection
- Python - Data Classes
- Python Errors & Exceptions
- Python - Syntax Errors
- Python - Exceptions
- Python - try-except Block
- Python - try-finally Block
- Python - Raising Exceptions
- Python - Exception Chaining
- Python - Nested try Block
- Python - User-defined Exception
- Python - Logging
- Python - Assertions
- Python - Warnings
- Python - Built-in Exceptions
- Python - Debugger (PDB)
- Python Multithreading
- Python - Multithreading
- Python - Thread Life Cycle
- Python - Creating a Thread
- Python - Starting a Thread
- Python - Joining Threads
- Python - Naming Thread
- Python - Thread Scheduling
- Python - Thread Pools
- Python - Main Thread
- Python - Thread Priority
- Python - Daemon Threads
- Python - Synchronizing Threads
- Python Synchronization
- Python - Inter-thread Communication
- Python - Thread Deadlock
- Python - Interrupting a Thread
- Python Networking
- Python - Networking
- Python - Socket Programming
- Python - URL Processing
- Python - Generics
- Python Libraries
- NumPy Tutorial
- Pandas Tutorial
- SciPy Tutorial
- Matplotlib Tutorial
- Django Tutorial
- OpenCV Tutorial
- Python Miscellenous
- Python - Date & Time
- Python - Maths
- Python - Iterators
- Python - Generators
- Python - Generator Expressions
- Python - Lambda Expressions
- Python - Closures
- Python - Decorators
- Python - Recursion
- Python - Reg Expressions
- Python - PIP
- Python - Database Access
- Python - Weak References
- Python - Serialization
- Python - Templating
- Python - Output Formatting
- Python - Performance Measurement
- Python - Data Compression
- Python - CGI Programming
- Python - XML Processing
- Python - GUI Programming
- Python - Command-Line Arguments
- Python - Docstrings
- Python - JSON
- Python - Sending Email
- Python - Further Extensions
- Python - Tools/Utilities
- Python - Odds and Ends
- Python - GUIs
- Python Advanced Concepts
- Python - Abstract Base Classes
- Python - Custom Exceptions
- Python - Higher Order Functions
- Python - Object Internals
- Python - Memory Management
- Python - Metaclasses
- Python - Metaprogramming with Metaclasses
- Python - Mocking and Stubbing
- Python - Monkey Patching
- Python - Signal Handling
- Python - Type Hints
- Python - Automation Tutorial
- Python - Humanize Package
- Python - Context Managers
- Python - Coroutines
- Python - Descriptors
- Python - Diagnosing and Fixing Memory Leaks
- Python - Immutable Data Structures
- Python - Domain Specific Language (DSL)
- Python - Data Model
- Python Useful Resources
- Python - Questions & Answers
- Python - Interview Questions & Answers
- Python - Online Quiz
- Python - Quick Guide
- Python - Reference
- Python - Cheatsheet
- Python - Projects
- Python - Useful Resources
- Python - Discussion
- Python Compiler
- NumPy Compiler
- Matplotlib Compiler
- SciPy Compiler
Python - Set Operators
Set Operators in Python
The set operators in Python are special symbols and functions that allow you to perform various operations on sets, such as union, intersection, difference, and symmetric difference. These operators provide a way to combine, compare, and modify sets.
Python implements them with following set operators −
Python Set Union Operator (|)
The union of two sets is a set containing all distinct elements that are in A or in B or both. For example,
{1,2}{2,3}={1,2,3}
The following diagram illustrates the union of two sets.
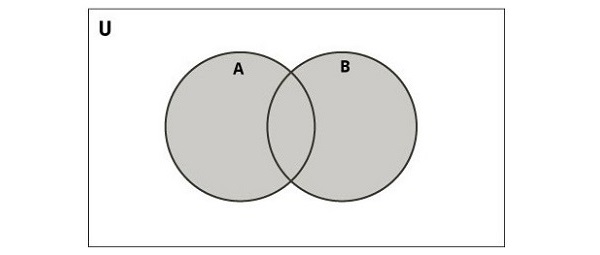
In Python, you can perform the union operation using the union() function or the | operator. This operation combines the elements of two sets while eliminating duplicates, resulting in a new set containing all unique elements from both sets −
Example
The following example uses the "|" operator and union() function, and returns the union of two sets −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 45, 73}
union_set1 = set1.union(set2)
union_set2 = set3 | set4
print ('The union of set1 and set2 is', union_set1)
print ('The union of set3 and set4 is', union_set2)
After executing the above code, we get the following output −
The union of set1 and set2 is {1, 2, 3, 4, 5}
The union of set3 and set4 is {73, 6, 8, 9, 45}
Python Set Intersection Operator (&)
The intersection of two sets AA and BB, denoted by A∩B, consists of all elements that are common to both in A and B. For example,
{1,2}∩{2,3}={2}
The following diagram illustrates intersection of two sets.
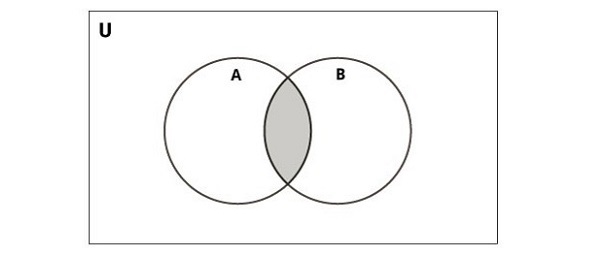
Python provides the intersection() function or the & operator to perform this operation. The resulting set contains only the elements present in both sets −
Example
Following example uses & operator and intersection() function, and returns intersection of two sets −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
intersection_set1 = set1.intersection(set2)
intersection_set2 = set3 & set4
print ('The intersection of set1 and set2 is', intersection_set1)
print ('The intersection of set3 and set4 is', intersection_set2)
It will produce the following output −
The intersection of set1 and set2 is {3}
The intersection of set3 and set4 is {8, 9}
Python Set Difference Operator (-)
The difference (subtraction) between two sets consists of elements present in the first set but not in the second set. It is defined as follows. The set AB consists of elements that are in A but not in B. For example,
If A={1,2,3} and B={3,5}, then AB={1,2}
The following diagram illustrates difference of two sets −
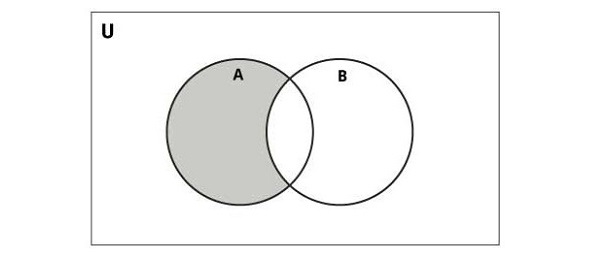
Python provides the difference() function or the - operator to perform this operation. The resulting set contains elements unique to the first set −
Example
The following example uses the "-" operator and the difference() function, and returns difference of two sets −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
difference_set1 = set1.difference(set2)
difference_set2 = set3 - set4
print ('The difference between set1 and set2 is', difference_set1)
print ('The difference between set3 and set4 is', difference_set2)
We get the output as shown below −
The difference between set1 and set2 is {1, 2}
The difference between set3 and set4 is {6}
Note that "s1-s2" is not the same as "s2-s1".
Python Set Symmetric Difference Operator
The symmetric difference of two sets consists of elements that are present in either set but not in both sets. The symmetric difference of A and B is denoted by "A Δ B" and is defined by −
A Δ B = (A − B) ⋃ (B − A)
If A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {1, 3, 5, 6, 7, 8, 9}, then A Δ B = {2, 4, 9}.
The following diagram illustrates the symmetric difference between two sets −
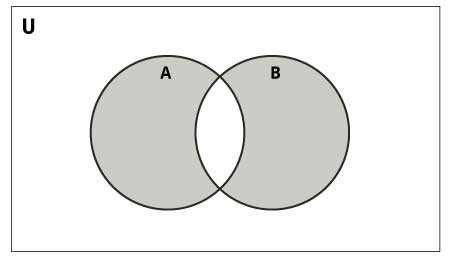
Python provides the symmetric_difference() function or the ^ operator to perform this operation. The resulting set contains elements that are unique to each set.
Example
The following example uses the "^" operator and the symmetric_difference() function, and returns symbolic difference of two sets −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
symmetric_difference_set1 = set1.symmetric_difference(set2)
symmetric_difference_set2 = set3 ^ set4
print ('The symmetric difference of set1 and set2 is', symmetric_difference_set1)
print ('The symmetric difference of set3 and set4 is', symmetric_difference_set2)
The result produced is as follows −
The symmetric difference of set1 and set2 is {1, 2, 4, 5}
The symmetric difference of set3 and set4 is {73, 6}
Python Subset Testing Operation
You can check whether one set is a subset of another using the issubset() function or the <= operator. A set A is considered a subset of another set B if all elements of A are also present in B −
Example
The following example uses the "<=" operator and the issubset() function, and returns subset testing of two sets −
set1 = {1, 2}
set2 = {1, 2, 3, 4}
set3 = {64, 47, 245, 48}
set4 = {64, 47, 3}
is_subset1 = set1.issubset(set2)
is_subset2 = set3 <= set4
print ('set1 is a subset of set2:', is_subset1)
print ('set3 is a subset of set4:', is_subset2)
The result produced is as follows −
set1 is a subset of set2: True set3 is a subset of set4: False