Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Simpson's 1/3 Rule for definite integral
Like the Trapezoidal Rule, Simpson’s 1/3rd rule is also used to find the integral value from the range a to b. The main difference between trapezoidal and the Simpson’s 1/3rd rule is, in the trapezoidal rule, the whole sections are divided into some trapezoids, but in this case, each trapezoid are also divided into two parts.
For this rule, we will follow this formula:
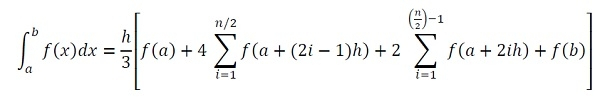
Here h is the width of the interval, and n is the number of intervals. We can find the h by using
Input and Output
Input: The function f(x): (x+(1/x). The lower and upper limit: 1, 2. The number of intervals: 20. Output: The answer is: 2.19315
Algorithm
integrateSimpson(a, b, n)
Input − The lower and upper limit of the integral and number of intervals n.
Output − The result after integration.
Begin h := (b - a)/n res := f(a) + f(b) lim := n/2 for i := 1 to lim, do oddSum := oddSum + f(a + (2i - 1)h) done oddSum := oddSum * 4 for i := 1 to lim-1, do evenSum := evenSum + f(a + 2ih) done evenSum := evenSum * 2 res := res + oddSum + evenSum res := res * (h/3) return res End
Example
#include<iostream>
#include<cmath>
using namespace std;
float mathFunc(float x) {
return (x+(1/x)); //function 1 + 1/x
}
float integrate(float a, float b, int n) {
float h, res = 0.0, oddSum = 0.0, evenSum = 0.0, lim;
int i;
h = (b-a)/n; //calculate the distance between two interval
res = (mathFunc(a)+mathFunc(b)); //initial sum using f(a) and f(b)
lim = n/2;
for(i = 1; i<=lim; i++)
oddSum += mathFunc(a+(2*i-1)*h); //sum of numbers, placed at odd number
oddSum *= 4; //odd sum are multiplied by 4
for(i = 1; i<lim; i++)
evenSum += mathFunc(a+(2*i)*h); //sum of numbers, placed at even number
evenSum *= 2; //even sum are multiplied by 2
res += oddSum+evenSum;
res *= (h/3);
return res; //The result of integration
}
main() {
float result, lowLim, upLim;
int interval;
cout << "Enter Lower Limit, Upper Limit and interval: ";
cin >>lowLim >>upLim >>interval;
result = integrate(lowLim, upLim, interval);
cout << "The answer is: " << result;
}Output
Enter Lower Limit, Upper Limit and interval: 1 2 20 The answer is: 2.19315
Updated on: 17-Jun-2020
689 Views
Advertisements