Teach with us

Projection Area of 3D Shapes

PythonServer Side ProgrammingProgramming

Suppose there is a N x N grid, we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z. Here each value v = grid[i][j] is showing a tower of v cubes placed on top of grid cell (i, j). We view the projection of these cubes onto the xy, yz, and zx planes. Here, we are viewing the projection when looking at the cubes from the top, the front, and the side view. We have to find the total area of all three projections.

So, if the input is like [[1,2],[3,4]]

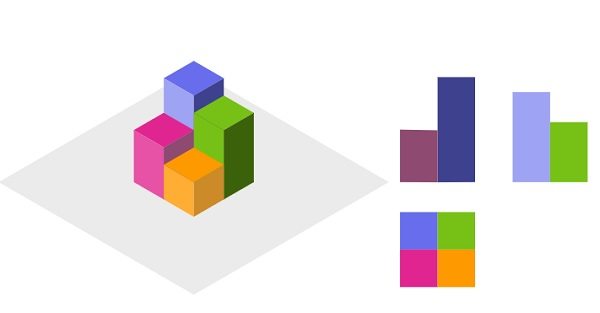
then the output will be 17.

To solve this, we will follow these steps −

  • xy := 0, yz := 0, xz := 0
  • for each row index r and row in grid, do
    • yz := yz + maximum of row
    • for each column index c and column col in row, do
      • if grid[r][c] > 0 is non-zero, then
        • xy := xy + 1
    • for each col in grid, do
      • xz := xz + maximum of col
  • return xy + yz + xz

Let us see the following implementation to get better understanding −

Example

 Live Demo

class Solution(object):
   def projectionArea(self, grid):
      xy = 0
      yz = 0
      xz = 0
      for r, row in enumerate(grid):
         yz += max(row)
         for c, col in enumerate(row):
            if grid[r][c] > 0:
               xy += 1
            for col in zip(*grid):
               xz += max(col)
      return xy + yz + xz
ob = Solution()
print(ob.projectionArea([[1,2],[3,4]]))

Input

[[1,2],[3,4]]

Output

17
raja
Arnab Chakraborty
Updated on 04-Jul-2020 10:21:08

Previous Page Print Page Next Page  
Advertisements