Program to find the diameter of a n-ary tree in Python

Suppose, we are given an n-ary tree and said to determine the diameter of the tree. The diameter of the tree is the longest path that is present between any two leaf nodes of the tree. We have to find out and return the integer value that represents the diameter of the tree.

So, if the input is like

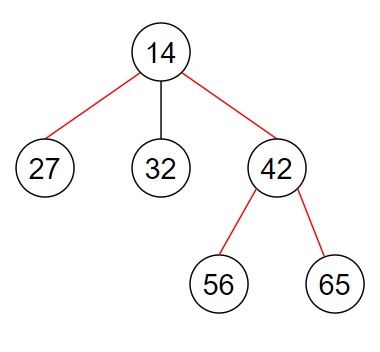
then the output will be 3.

The diameter of this n-ary tree consists of the edges 27->14, 14->42, and 42->56 or 42->65 (marked in the diagram by red lines). The path length is 3.

To solve this, we will follow these steps −

• ans := 1

• Define a function depth() . This will take root

  • if root is not empty, then

    • return 0

  • children := a new list containing values 0, 0

  • temp_children := a new list

  • for each child in children of the root, do

    • insert depth(child) at the end of temp_children

  • if size of (temp_children) > 0, then

    • children := temp_children

  • ans := maximum of ans, sum(sort the list children [from index length of (children)- 2 to end]) + 1

  • return maximum of children + 1

• depth(root)

• return(ans -1)

Example (Python)

Let us see the following implementation to get better understanding −

 Live Demo

class Node:
   def __init__(self, value, child = None) -> None:
      self.val = value
      self.children = []
      if child != None:
         for value in child:
            self.children.append(value)

ans = 1
def solve(root):
   def depth(root):
      global ans
      if not root:
         return 0
      children = [0, 0]
      temp_children = [depth(child) for child in root.children]
      if len(temp_children) > 0:
         children = temp_children
      ans = max(ans, sum(sorted(children)[-2:]) + 1)

      return max(children) + 1
   depth(root)

   return ans -1

node6 = Node(65)
node5 = Node(56)
node4 = Node(42, [node5, node6])
node3 = Node(32)
node2 = Node(27)
node1 = Node(14, [node2, node3, node4])
root = node1

print(solve(root))

Input

node6 = Node(65)
node5 = Node(56)
node4 = Node(42, [node5, node6])
node3 = Node(32)
node2 = Node(27)
node1 = Node(14, [node2, node3, node4])
root = node1

Output

3