Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Serialize and Deserialize N-ary Tree in C++
Suppose we have one N-ary tree and we have to serialize and deserialize them. As we know that the serialization is the process of converting a data structure or object into a sequence of bits so we can store them in a file or memory buffer, and that can be reconstructed later in the same or another computer environment.
Here we have to devise an algorithm to serialize and deserialize an N-ary tree. The N-ary tree is a rooted tree in which each node has no more than N children.
So, if the input is like
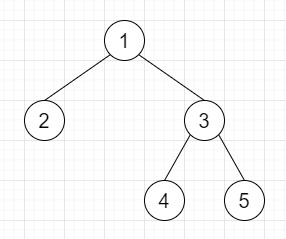
then the output will be Serialize: 1 #3 2 4 #5 6 ##### and Deserialized Tree: 1[3[5, 6, ], 2, 4, ]
To solve this, we will follow these steps −
Define a function createVector(), this will take s,
Define one 2D array ret
Define an array tempv
temp := empty string
for initialize i := 0, when i < size of s, update (increase i by 1), do −
if s[i] is not equal to blank space and s[i] is not equal to '#', then −
temp := temp + s[i]
otherwise when s[i] is same as blank string, then −
insert temp s integer at the end of tempv
temp := empty string
otherwise when s[i] is same as '#', then −
insert tempv at the end of ret
temp := empty string
clear tempv
while (not ret is empty and last element of ret is same as 0), do −
delete last element from ret
return ret
Define a function serialize(), this will take root,
ret := empty string
if not root is non-zero, then −
return ret
Define one queue q
insert root into q
rret := ret concatenate val of root
ret := ret concatenate space
ret := ret concatenate "#"
while (not q is empty), do −
curr = first element of q
delete element from q
for initialize i := 0, when i < size of the children array of curr, update (increase i by 1), do −
if children[i] of curr, then −
ret := ret concatenate children[i] of curr
insert children[i] of curr into q
ret := ret + blank string
ret := ret concatenate "#"
return ret
Define a function deserialize(), this will take data,
if size of data is same as 0, then −
return null
Define one 2D array v := createVector(data)
ret := new node with value v[0, 0]
Define one queue q
insert ret into q
i := 1
while (not q is empty and i − size of v), do −
curr = first element of q
delete element from q
for initialize j := 0, when j − size of v[i],update (increase j by 1), do −
node := v[i, j]
temp = new node with value node
insert temp at the end of children of curr
insert temp into q
(increase i by 1)
return ret
Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
string n_ary_to_str(Node *root){
string ret = "";
if(root){
ret = ret + to_string(root->val);
if(root->children.size() > 0){
ret += "[";
for(Node* child : root->children){
ret += n_ary_to_str(child) + ", ";
}
ret += "]";
}
}
return ret;
}
class Codec {
public:
vector<vector<int>>createVector(string s) {
vector<vector<int>> ret;
vector<int> tempv;
string temp = "";
for (int i = 0; i < s.size(); i++) {
if (s[i] != ' ' && s[i] != '#') {
temp += s[i];
}
else if (s[i] == ' ') {
tempv.push_back(stoi(temp));
temp = "";
}
else if (s[i] == '#') {
ret.push_back(tempv);
temp = "";
tempv.clear();
}
}
while (!ret.empty() && ret.back().size() == 0)
ret.pop_back();
return ret;
}
string serialize(Node *root) {
string ret = "";
if (!root)
return ret;
queue<Node *> q;
q.push(root);
ret += to_string(root->val);
ret += " ";
ret += "#";
while (!q.empty()) {
Node *curr = q.front();
q.pop();
for (int i = 0; i < curr->children.size(); i++) {
if (curr->children[i]) {
ret += to_string(curr->children[i]->val);
q.push(curr->children[i]);
}
ret += " ";
}
ret += "#";
}
return ret;
}
Node *deserialize(string data) {
Node *ret;
if (data.size() == 0)
return NULL;
vector<vector<int>> v = createVector(data);
ret = new Node(v[0][0]);
queue<Node *> q;
q.push(ret);
int i = 1;
while (!q.empty() && i < v.size()) {
Node *curr = q.front();
q.pop();
for (int j = 0; j < v[i].size(); j++) {
int node = v[i][j];
Node *temp = new Node(node);
curr->children.push_back(temp);
q.push(temp);
}
i++;
}
return ret;
}
};
main() {
Codec ob;
Node n5(5), n6(6);
Node n3(3); n3.children.push_back(&n5); n3.children.push_back(&n6);
Node n2(2), n4(4);
Node n1(1); n1.children.push_back(&n3); n1.children.push_back(&n2);
n1.children.push_back(&n4);
cout << "Given Tree: " << n_ary_to_str(&n1) << endl;
string ser = ob.serialize(&n1);
cout << "Serialize: " << ser << endl;
Node *deser = ob.deserialize(ser);
cout << "Deserialized Tree: " << n_ary_to_str(deser);
}Input
Node n5(5), n6(6); Node n3(3); n3.children.push_back(&n5); n3.children.push_back(&n6); Node n2(2), n4(4); Node n1(1); n1.children.push_back(&n3); n1.children.push_back(&n2); n1.children.push_back(&n4);
Output
Given Tree: 1[3[5, 6, ], 2, 4, ] Serialize: 1 #3 2 4 #5 6 ##### Deserialized Tree: 1[3[5, 6, ], 2, 4, ]
319 Views
