Program to find out the sum of minimum cost within a graph among all vertices in Python

Suppose there is a weighted graph with n vertices and m edges. The edges have the weights in powers of 2. Any vertex can be reached from any vertex in the graph, and the cost of travel will be the addition of all the edge weights in the graph. We shall have to determine the sum of minimum cost between each pair of vertices.

So, if the input is like

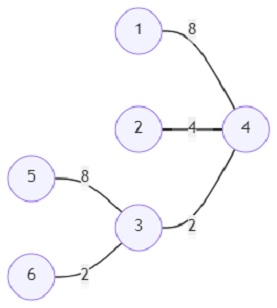
and number of vertices (n) = 6; then the output will be 2696.

The sum of all the distances is 2696.

To solve this, we will follow these steps −

• Define a function par_finder() . This will take i, par
  • if par[i] is same as -1, then
    • return i
  • res := par_finder(par[i], par)
  • par[i] := res
  • return res
• Define a function helper() . This will take i, par, w, G, n
  • child := 1
  • for each item in G[i], do
    • if item[0] is same as par, then
      • go for next iteration
    • otherwise,
      • child := child + helper(item[0], i, item[1], G, n)
    • if par is not same as -1, then
      • ans := ans + child * (n - child) *(1 * 2^w)
    • return child
• G := a new list containing n + 1 other lists
• edges := a new list
• for each item in roads, do
  • u := item[0]
  • v := item[1]
  • w := item[2]
  • insert (u-1, v-1, w) at the end of edges
• sort the list edges by the edge weights
• par := a new list of size n + 1 initialized with -1
• r_edge := a new list
• for each i in edges, do
  • if par_finder(i[0], par) is same as par_finder(i[1], par), then
    • go for next iteration
  • otherwise,
    • insert i at the end of r_edge
    • insert pair (i[1],i[2]) at the end of G[i[0]]
    • insert pair (i[0],i[2]) at the end of G[i[1]]
    • par[par_finder(i[0], par)] := par_finder(i[1], par)
• ans := 0
• helper(0, -1, 0, G, n)
• return ans

Example

Let us see the following implementation to get better understanding −

def par_finder(i, par) :
    if par[i] == -1 :
         return i
    res = par_finder(par[i], par)
    par[i] = res
    return res

def helper(i, par, w, G, n) :
    global ans
    child = 1
    for item in G[i] :
        if item[0] == par :
            continue
        else :
            child += helper(item[0],i,item[1], G, n)
    if par != -1 :
        ans += child * (n - child) * (1 << w)
    return child

def solve(n, roads):
    global ans
    G = [[] for i in range(n + 1)]
    edges = []
    for item in roads :
        u,v,w = map(int, item)
        edges.append((u-1, v-1, w))
    edges = sorted(edges,key = lambda item : item[2])
    par = [-1 for i in range(n + 1)]
    r_edge = []
    for i in edges :
        if par_finder(i[0], par) == par_finder(i[1], par) :
            continue
        else :
            r_edge.append(i)
            G[i[0]].append((i[1],i[2]))
            G[i[1]].append((i[0],i[2]))
            par[par_finder(i[0], par)] = par_finder(i[1], par)
    ans = 0      
    helper(0, -1, 0, G, n)
    return ans

print(solve(6, [(1,4,8), (2,4,4), (3,4,4), (3,4,2), (5,3,8), (6,3,2)]))

Input

6, [(1,4,8), (2,4,4), (3,4,4), (3,4,2), (5,3,8), (6,3,2)]

Output

2696

Arnab Chakraborty

Updated on: 06-Oct-2021

345 Views

Kickstart Your Career

Get certified by completing the course

Get Started