Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find largest color value in a directed graph in Python
Suppose we have a directed graph with n colored nodes and m different edges. And the nodes are numbered from 0 to n-1. We have a string col with lowercase letters, where col[i] represents the color of the ith node in this graph (0-indexed). We also have an edge list where edges[j] = (u, v) represents, there is an edge between u and v.
A valid path in the graph is a sequence of nodes xi for all i from 1 to k, such that there is a directed edge from xi to xi+1. The color of the path is the most frequent node color of that path. We have to find largest color value of any valid path in that graph. If there is a cycle in the graph then return -1.
So, if the input is like col = "aabada" edges = [(0,1),(1,4),(1,2),(2,3),(3,5),(4,5)],
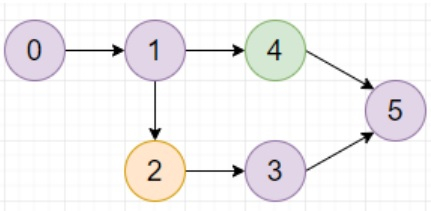
then the output will be 4 as 0 -> 1 -> 2 -> 3 -> 5 has longest path with color 'a'.
To solve this, we will follow these steps −
n:= size of col
graph:= given graph from the edge list
indegree:= map containing nodes and their in-degree values
queue:= a new list
dp:= make an array of size n x 26, and fill with 0
colorvalues:= make a list with order of c in alphabet for all c in col
for u in range 0 to n - 1, do
if u is not in indegree, then
insert u at the end of queue
dp[u, colorvalues[u]]:= 1
visited:= 0
while queue is not empty, do
u:= front element of queue and delete it after
visited := visited + 1
for each v in graph[u], do
for c in range 0 to 25, do
dp[v, c] = maximum of dp[v, c] and (dp[u, c] + (1 if c is same as colorvalues[v], otherwise 0)
indegree[v] := indegree[v] - 1
if indegree[v] is same as 0, then
insert v at the end of queue
del indegree[v]
if visited < n, then
return -1
return maximum element in dp
Example
Let us see the following implementation to get better understanding
from collections import defaultdict
def solve(col, edges):
n=len(col)
graph=defaultdict(list)
indegree=defaultdict(int)
for u,v in edges:
graph[u].append(v)
indegree[v]+=1
queue=[]
dp=[[0]*26 for _ in range(n)]
colorvalues=[ord(c)-ord("a") for c in col]
for u in range(n):
if u not in indegree:
queue.append(u)
dp[u][colorvalues[u]]=1
visited=0
while queue:
u=queue.pop()
visited+=1
for v in graph[u]:
for c in range(26):
dp[v][c]=max(dp[v][c],dp[u][c] + (c==colorvalues[v]))
indegree[v]-=1
if indegree[v]==0:
queue.append(v)
del indegree[v]
if visited<n:
return -1
return max(max(x) for x in dp)
col = "aabada"
edges = [(0,1),(1,4),(1,2),(2,3),(3,5),(4,5)]
print(solve(col, edges))Input
"aabada", [(0,1),(1,4),(1,2),(2,3),(3,5),(4,5)]
Output
4
261 Views
