Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Shortest Path in a Directed Acyclic Graph
One weighted directed acyclic graph is given. Another source vertex is also provided. Now we have to find the shortest distance from the starting node to all other vertices, in the graph.
To detect Smaller distance, we can use another algorithm like Bellman-Ford for the graph with negative weight, for positive weight the Dijkstra’s algorithm is also helpful. Here for Directed Acyclic Graph, we will use the topological sorting technique to reduce complexity.
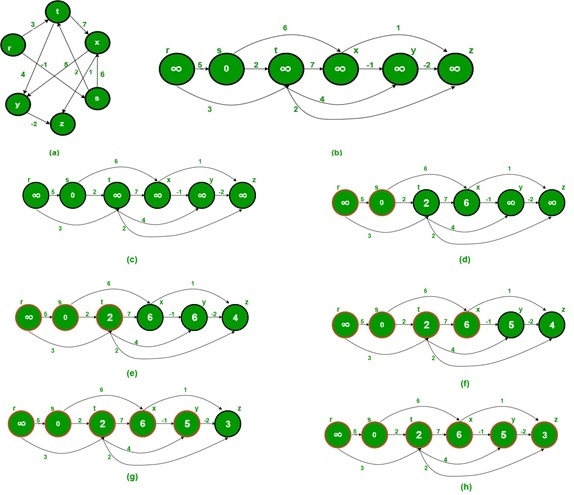
Input and Output
Input: The cost matrix of the graph. 0 5 3 -∞ -∞ -∞ -∞ 0 2 6 -∞ -∞ -∞ -∞ 0 7 4 2 -∞ -∞ -∞ 0 -1 1 -∞ -∞ -∞ -∞ 0 -2 -∞ -∞ -∞ -∞ -∞ 0 Output: Shortest Distance from Source Vertex 1 Infinity 0 2 6 5 3
Algorithm
topoSort(u, visited, stack)
Input: starting node u, the visited list to keep track, the stack.
Output: Sort the nodes in a topological way.
Begin mark u as visited for all vertex v, which is connected with u, do if v is not visited, then topoSort(v, visited, stack) done push u into the stack End
shortestPath(start)
Input − The starting node.
Output − List of the shortest distance of all vertices from the starting node.
Begin initially make all nodes as unvisited for each node i, in the graph, do if i is not visited, then topoSort(i, visited, stack) done make distance of all vertices as ∞ dist[start] := 0 while stack is not empty, do pop stack item and take into nextVert if dist[nextVert] ≠∞, then for each vertices v, which is adjacent with nextVert, do if cost[nextVert, v] ≠∞, then if dist[v] > dist[nectVert] + cost[nextVert, v], then dist[v] := dist[nectVert] + cost[nextVert, v] done done for all vertices i in the graph, do if dist[i] = ∞, then display Infinity else display dist[i] done End
Example
#include<iostream>
#include<stack>
#define NODE 6
#define INF 9999
using namespace std;
int cost[NODE][NODE] = {
{0, 5, 3, INF, INF, INF},
{INF, 0, 2, 6, INF, INF},
{INF, INF, 0, 7, 4, 2},
{INF, INF, INF, 0, -1, 1},
{INF, INF, INF, INF, 0, -2},
{INF, INF, INF, INF, INF, 0}
};
void topoSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<NODE; v++) {
if(cost[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topoSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void shortestPath(int start) {
stack<int> stk;
int dist[NODE];
bool vis[NODE];
for(int i = 0; i<NODE;i++)
vis[i] = false; // make all nodes as unvisited at first
for(int i = 0; i<NODE; i++) //perform topological sort for vertices
if(!vis[i])
topoSort(i, vis, stk);
for(int i = 0; i<NODE; i++)
dist[i] = INF; //initially all distances are infinity
dist[start] = 0; //distance for start vertex is 0
while(!stk.empty()) { //when stack contains element, process in topological order
int nextVert = stk.top(); stk.pop();
if(dist[nextVert] != INF) {
for(int v = 0; v<NODE; v++) {
if(cost[nextVert][v] && cost[nextVert][v] != INF){ if(dist[v] > dist[nextVert] +cost[nextVert][v])dist[v] = dist[nextVert] + cost[nextVert][v];
}
}
}
for(int i = 0; i<NODE; i++)
(dist[i] == INF)?cout << "Infinity ":cout << dist[i]<<" ";
}
main() {
int start = 1;
cout << "Shortest Distance From Source Vertex "<<start<<endl;
shortestPath(start);
}Output
Shortest Distance From Source Vertex 1 Infinity 0 2 6 5 3
Updated on: 16-Jun-2020
870 Views
Advertisements