
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Euler Circuit in a Directed Graph
The Euler path is a path, by which we can visit every edge exactly once. We can use the same vertices for multiple times. The Euler Circuit is a special type of Euler path. When the starting vertex of the Euler path is also connected with the ending vertex of that path, then it is called the Euler Circuit.
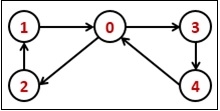
To check whether a graph is Eulerian or not, we have to check two conditions −
- The graph must be connected.
- The in-degree and out-degree of each vertex must be the same.
Input and Output
Input: Adjacency matrix of the graph. 0 1 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 Output: Euler Circuit Found.
Algorithm
traverse(u, visited)
Input: The start node u and the visited node to mark which node is visited.
Output: Traverse all connected vertices.
Begin mark u as visited for all vertex v, if it is adjacent with u, do if v is not visited, then traverse(v, visited) done End
isConnected(graph)
Input − The graph.
Output − True if the graph is connected.
Begin define visited array for all vertices u in the graph, do make all nodes unvisited traverse(u, visited) if any unvisited node is still remaining, then return false done return true End
isEulerCircuit(Graph)
Input: The given Graph.
Output: True when one Euler circuit is found.
Begin if isConnected() is false, then return false define list for inward and outward edge count for each node for all vertex i in the graph, do sum := 0 for all vertex j which are connected with i, do inward edges for vertex i increased increase sum done number of outward of vertex i is sum done if inward list and outward list are same, then return true otherwise return false End
Example
#include<iostream>
#include<vector>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 0, 0, 0},
{0, 0, 1, 0, 0},
{0, 0, 0, 1, 1},
{1, 0, 0, 0, 0},
{0, 0, 1, 0, 0}
};
void traverse(int u, bool visited[]) {
visited[u] = true; //mark v as visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) {
if(!visited[v])
traverse(v, visited);
}
}
}
bool isConnected() {
bool *vis = new bool[NODE];
//for all vertex u as start point, check whether all nodes are visible or not
for(int u; u < NODE; u++) {
for(int i = 0; i<NODE; i++)
vis[i] = false; //initialize as no node is visited
traverse(u, vis);
for(int i = 0; i<NODE; i++) {
if(!vis[i]) //if there is a node, not visited by traversal, graph is not connected
return false;
}
}
return true;
}
bool isEulerCircuit() {
if(isConnected() == false) { //when graph is not connected
return false;
}
vector<int> inward(NODE, 0), outward(NODE, 0);
for(int i = 0; i<NODE; i++) {
int sum = 0;
for(int j = 0; j<NODE; j++) {
if(graph[i][j]) {
inward[j]++; //increase inward edge for destination vertex
sum++; //how many outward edge
}
}
outward[i] = sum;
}
if(inward == outward) //when number inward edges and outward edges for each node is same
return true;
return false;
}
int main() {
if(isEulerCircuit())
cout << "Euler Circuit Found.";
else
cout << "There is no Euler Circuit.";
}
Output
Euler Circuit Found.

Advertisements
