Program to count number of isosceles triangle from colored vertex regular polygon in Python

Suppose we have one regular polygon with n sides represented as a binary string of size n. The vertices can be colored either in blue (0) or in red (1). They are colored in clockwise direction We have to count number of isosceles triangles whose vertices are vertices of the regular polygon, and their colors are same.

So, if the input is like polygon = "111010", then the output will be 2 because

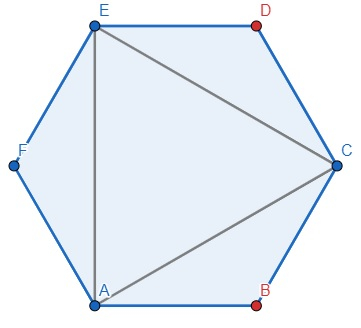
there are two triangles ACE and AFE.

To solve this, we will follow these steps −

  • Define a function all() . This will take n
  • if n mod 2 is same as 1, then, no := n*(n-1) /2
  • otherwise, no := n*(n/2-1)
  • if n mod 3 is same as 0, then no := no - n/3*2
  • return no
  • Define a function non() . This will take a,n
  • if n mod 2 is same as 1, then
    • s0 := 0, s1 := 0
    • i := 0
    • while i < n, do
      • if a[i] is same as '0', then s0 := s0 + 1
      • otherwise s1 := s1 + 1
      • i := i + 1
    • s := s0*s1*6
    • if n mod 3 is same as 0, then
      • n1 := n/3
      • n2 := n1*2
      • i := 0
      • while i < n, do
        • if a[i] is not same as a[(i+n1)mod n], then
          • s := s - 2
        • if a[i] is not same as a[(i+n2)mod n], then
          • s := s - 2
        • i := i + 1
  • otherwise,
    • s00 := 0, s01 := 0, s10 := 0, s11 := 0, s := 0
    • i := 0
    • while i < n, do
      • if a[i] is same as '0', then, s00 := s00 + 1
      • otherwise s01 := s01 + 1
      • i := i + 2
    • i := 1
    • while i < n, do
      • if a[i] is same as '0', then, s10 := s10 + 1
      • otherwise s11 := s11 + 1
      • i := i + 2
    • s := s + s00 * s01 * 8
    • s := s + s10 * s11 * 8
    • s := s + s00 * s11 * 4
    • s := s + s10 * s01 * 4
    • n1 := n/2
    • i := 0
    • while i < n, do
      • if a[i] is not same as a[(i + n1)mod n], then
        • s := s - 2
      • i := i + 1
    • if n mod 3 is same as 0, then
      • n1 := n/3
      • n2 := n1*2
      • i := 0
      • while i < n, do
        • if a[i] is not same as a[(i+n1)mod n], then
          • s := s - 2
        • if a[i] is not same as a[(i+n2)mod n], then
          • s := s - 2
        • i := i + 1
  • return s/2
  • From the main method, do the following −
  • n := size of polygon
  • no := all(n) - non(polygon, n) /2
  • return no

Example

Let us see the following implementation to get better understanding −

def all(n):
   if n % 2 == 1:
      no = n*(n-1)/2
   else:
      no = n*(n/2-1)
   if n % 3 == 0:
      no -= n/3*2
   return no

def non(a,n):
   if n % 2 == 1:
      s0 = s1 = 0
      i = 0
      while i < n:
         if a[i] == '0':
            s0 += 1
         else:
            s1 += 1
         i += 1
      s = s0*s1*6
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i<n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   else:
      s00 = s01 = s10 = s11 = s = 0
      i = 0
      while i <n:
         if a[i] == '0':
            s00 += 1
         else:
            s01 += 1
         i += 2
      i = 1
      while i < n:
         if a[i] == '0':
            s10 += 1
         else:
            s11 += 1
         i += 2
      s += s00 * s01 * 8
      s += s10 * s11 * 8
      s += s00 * s11 * 4
      s += s10 * s01 * 4
      n1 = n/2
      i = 0
      while i < n:
         if a[i] != a[int((i + n1)%n)]:
            s -= 2
         i += 1
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i < n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   return s/2

def solve(polygon):
   n = len(polygon)
   no = all(n) - non(polygon,n)/2
   return int(no)

polygon = "111010"
print(solve(polygon))

Input

1, 1000

Output

2

Updated on: 11-Oct-2021

132 Views

Kickstart Your Career

Get certified by completing the course

Get Started
Advertisements