Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to count minimum semesters to cover all different courses in Python
Suppose we have a number n, indicates that there are n different courses labeled from 1 to n. We also have an array called relations where relations[i] contains a pair (prevCourse_i, nextCourse_i), representing a prerequisite relationship between the course prevCourse_i and the course nextCourse_i: so course prevCourse_i has to be taken before the course nextCourse_i. And the last parameter we have that is k. In one semester, we can take at most k number of courses as long as we have taken all the prerequisites in the previous semester for the courses we are taking. We have to find the minimum number of semesters needed to take all courses.
So, if the input is like
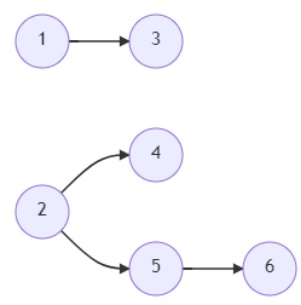
then the output will be 3 because in the first semester we can take course 1 and 2, now we are eligible for course 3, 4 and 5, so if we take 5 and any one of 3 or 4 for the second semester, then we can end all courses in the next semester. So we need 3 semesters in total
To solve this, we will follow these steps −
taken := a new set
g1 := a list with n empty lists
g2 := a new list of size n and fill with 0
w := a new list of size n and fill with 0
semester := 0
for each x in relations, do
insert x[0]-1 at the end of g1[x[1]-1]
insert x[1]-1 at the end of g2[x[0]-1]
weight := a new list from the length of all items in g1
for i in range 0 to n - 1, do
for each x in g1[i], do
w[x] := maximum of w[x] and weight[i]
while size of taken < n, do
courses := a new list
for i in range 0 to n - 1, do
if g1[i] is empty and i is not in taken, then
insert (i, w[i]) at the end of courses
if size of courses > k, then
courses = sort courses based on the second parameter in reverse order
courses := list of first k courses
semester := semester + 1
for each x in courses, do
for each y in g2[x[0]], do
delete x[0] from g1[y]
g2[x[0]] := empty list
insert x[0] into taken
return semester
Example
Let us see the following implementation to get better understanding
def solve(n, relations, k):
taken = set()
g1 = [[] for _ in range(n)]
g2 = [[] for _ in range(n)]
w = [0] * n
semester = 0
for x in relations:
g1[x[1]-1].append(x[0]-1)
g2[x[0]-1].append(x[1]-1)
weight = list(map(len, g1))
for i in range(n):
for x in g1[i]:
w[x] = max(w[x], weight[i])
while len(taken) < n:
courses = []
for i in range(n):
if (not g1[i]) and (i not in taken):
courses.append([i,w[i]])
if len(courses) > k:
courses = sorted(courses, key = lambda x:x[1],reverse=True)
courses = courses[:k]
semester += 1
for x in courses:
for y in g2[x[0]]:
g1[y].remove(x[0])
g2[x[0]] = []
taken.add(x[0])
return semester
n = 6
relations = [(1,3),(2,5),(2,4),(5,6)]
k = 2
print(solve(n, relations, k))Input
6, [(1,3),(2,5),(2,4),(5,6)], 2
Output
3
227 Views
