Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find out the minimum path to deliver all letters in Python
Suppose there are n cities and that are connected with n -1 roads. A city can be visited from any other city. Now the postal system of the cities delivers k letters daily. The letter's destination can be any of the k different cities. A postal worker has to deliver all the letters to their addresses each day. We shall have to find out the minimum distance the worker has to travel to deliver all the letters. The worker can start from any given city.
So, if the input is like
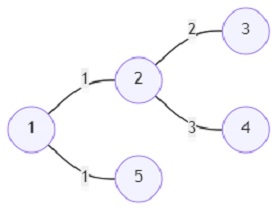
and the letters have to be delivered in cities (delv) 1, 2, and 4; then the output will be 4.
The worker can start delivering either from cities 1, 2, or 4. If the worker starts at city 1, then the path will be 1->2->4, vice-versa in the case of city 4; 4->2->1. The total cost will be 1 + 3 = 4. If he starts from city 2, the cost will be greater than the other two.
To solve this, we will follow these steps −
- Define a function depth_search() . This will take node, p
- d1 := -infinity
- d2 := -infinity
- for each pair x, y in adj_list[node], do
- if x is not same as p, then
- d1 := maximum of (d1, depth_search(x, node) + y)
- if d1 > d2, then
- swap the values of d2 and d1
- ti[node] := ti[node] + ti[x]
- if 0 < ti[x] < k, then
- SUM := SUM + y
- if d1 > 0, then
- MAX := maximum of (MAX, d1 + d2)
- if d2 > 0 and tj[node] is non-zero, then
- MAX := maximum of(MAX, d2)
- if tj[node] is non-zero, then
- d2 := max(0, d2)
- return d2
- if x is not same as p, then
- k := size of delv
- adj_list := a new map
- ti := a new list of size (nodes + 5) initialized with 0
- tj := a new list of size (nodes + 5) initialized with 0
- for each i in delv, do
- ti[i] := 1
- tj[i] := 1
- for each item in roads, do
- x := item[0]
- y := item[1]
- c := item[2]
- if x is not present in adj_list, then
- adj_list[x] := []
- if y is not present in adj_list, then
- adj_list[y] := []
- append (y, c) at the end of adj_list[x]
- append (x, c) at the end of adj_list[y]
- SUM := 0
- MAX := 0
- depth_search(1, 1)
- return SUM * 2 - MAX
Example
Let us see the following implementation to get better understanding −
import sys
from math import inf as INF
sys.setrecursionlimit(10**5 + 5)
def depth_search(node, p):
global SUM, MAX
d1 = -INF
d2 = -INF
for x, y in adj_list[node]:
if x != p:
d1 = max(d1, depth_search(x, node) + y)
if d1 > d2:
d1, d2 = d2, d1
ti[node] += ti[x]
if 0 < ti[x] < k:
SUM += y
if d1 > 0: MAX = max(MAX, d1 + d2)
if d2 > 0 and tj[node]: MAX = max(MAX, d2)
if tj[node]: d2 = max(0, d2)
return d2
def solve(nodes, delv, roads):
global k, ti, tj, adj_list, SUM, MAX
k = len(delv)
adj_list = {}
ti = [0] * (nodes + 5)
tj = [0] * (nodes + 5)
for i in delv:
ti[i] = tj[i] = 1
for item in roads:
x, y, c = map(int, item)
if x not in adj_list: adj_list[x] = []
if y not in adj_list: adj_list[y] = []
adj_list[x].append([y, c])
adj_list[y].append([x, c])
SUM = 0
MAX = 0
depth_search(1,1)
return SUM * 2 - MAX
print(solve(5, [1, 2, 4], [(1,2,1),(2,3,2),(2,4,3),(1,5,1)]))
Input
5, [1, 2, 4], [(1,2,1),(2,3,2),(2,4,3),(1,5,1)]
Output
4
116 Views
To Continue Learning Please Login