
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
One’s Complement
Binary Number System is one the type of most popular Number Representation techniques that used in digital systems. In the Binary System, there are only two symbols or possible digit values, i.e., 0 (off) and 1 (on). Represented by any device that only 2 operating states or possible conditions.
Generally, there are two types of complement of Binary number: 1’s complement and 2’s complement. To get 1’s complement of a binary number, simply invert the given number. For example, 1’s complement of binary number 110010 is 001101. To get 2’s complement of binary number is 1’s complement of given number plus 1 to the least significant bit (LSB). For example 2’s complement of binary number 10010 is (01101) + 1 = 01110.
1’s Complement of a Binary Number:
There is a simple algorithm to convert a binary number into 1’s complement. To get 1’s complement of a binary number, simply invert the given number. You can simply implement logic circuit using only NOT gate for each bit of Binary number input. Implementation of logic circuit of 4-bit 1’s complement is given as following below.

Example-1: Find 1’s complement of binary number 10101110.
Simply invert each bit of given binary number, so 1’s complement of given number will be 01010001.
Example-2: Find 1’s complement of binary number 10001.001.
Simply invert each bit of given binary number, so 1’s complement of given number will be 01110.110.
Example-3: Find 1’s complement of each 3 bit binary number.
Simply invert each bit of given binary number, so 1’s complement of each 3 bit binary number will be,
|
Binary number |
1’s complement |
|---|---|
| 000 |
111 |
| 001 |
110 |
| 010 |
101 |
| 011 |
100 |
| 100 |
011 |
| 101 |
010 |
| 110 |
001 |
| 111 |
000 |
Uses of 1’s Complement Binary Numbers:
There are various uses of 1’s complement of Binary numbers, mainly in signed Binary number representation and various arithmetic operations for Binary numbers, e.g., additions, subtractions, etc.
1’s Complementation in Signed Binary number Representation:
1’s complement binary numbers are very useful in Signed number representation. Positive numbers are simply represented as Binary number number. There is nothing to do for positive binary number. But in case of negative binary number representation, we represent in 1’s complement. If the number is negative then it is represented using 1’s complement. First represent the number with positive sign and then take 1’s complement of that number.
Example: Let we are using 5 bits register. The representation of -5 and +5 will be as follows:
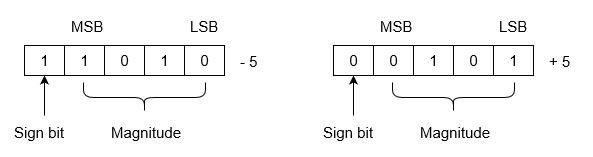
+5 is represented as it is represented in sign magnitude method. -5 is represented using the following steps:
(i) +5 = 0 0101
(ii) Take 1’s complement of 0 0101 and that is 1 1010. MSB is 1 which indicates that number is negative.
MSB is always 1 in case of negative numbers.
Range of Numbers: For k bits register, positive largest number that can be stored is ( 2 (k-1) -1) and negative lowest number that can be stored is -( 2 (k-1) -1).
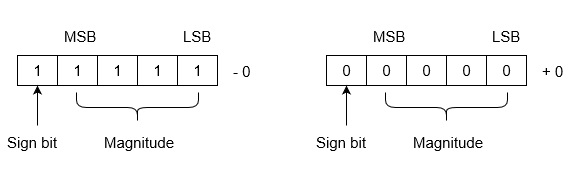
Note that drawback of this system is that 0 has two different representation one is -0 (e.g., 1 1111 in five bit register) and second is +0 (e.g., 0 0000 in five bit register).
Lets see arithmetic operations: Subtractions and Additions in 1’s complement binary numbers.
Subtractions by 1’s Complement:
The algorithm to subtract two binary number using 1’s complement is explained as following below:
- Take 1’s complement of the subtrahend
- Add with minuend
- If the result of above addition has carry bit 1, then add it to the least significant bit (LSB) of given result
- If there is no carry bit 1, then take 1’s complement of the result which will be negative
Note that subtrahend is number that to be subtracted from the another number, i.e., minuend.
Example (Case-1: When Carry bit 1): Evaluate 10101 - 00101
According to above algorithm, take 1’s complement of subtrahend 00101, which will be 11010, then add both of these. So, 10101 + 11010 =1 01111 . Since, there is carry bit 1, so add this to the LSB of given result, i.e., 01111+1=10000 which is the answer.
Example (Case-2: When no Carry bit): Evaluate 11110 with 1110
According to above algorithm, take 1’s complement of subtrahend 11110, which will be 00011. Then add both of these, So, 11001 + 00011 =11100 . Since there is no carry bit 1, so take 1’s complement of above result, which will be 00011, and this is negative number, i.e, 00011, which is the answer.
Similarly, you can subtract two mixed (with fractional part) binary numbers. Note that you always add Carry bit the the least significant bit (LSB) of the result, whenever you get carry bit 1. LSB of fractional binary number is last (rightmost) bit of mixed or fractional binary numbers.
Additions by 1’s Complement:
There are difference scenario for addition of two binary numbers using 1’s complement. These are explained as following below.
Case-1: Addition of positive and negative number when positive number has greater magnitude:
When positive number has greater magnitude, then take simply 1’s complement of negative number and the end-around carry of the sum is added to the least significant bit (LSB).
Example: Add 1110 and -1101.
So, take 1’s complement of 1101, which will be 0010, then add with given number. So, 1110+0010=1 0000 , then add this carry bit to the LSB, 0000+1=0001 , which is the answer.
Note that if the register size is big then fill the same value of MSB to preserve sign magnitude for inputs and output.
Case-2: Addition of positive and negative number when negative number has greater magnitude:
When the negative number has greater magnitude, then take 1’s complement of negative number and add with given positive number. Since there will not be any end-around carry bit, so take 1’s complement of the result and this result will be negative.
Example: Add 1010 and -1100 in five-bit registers.
Note that there are five-bit registers, so these new numbers will be 01010 and -01100.
Now take 1’s complement of 01100 which will be 10011 and add 01010+10011=11101 . Then take 1’s complement of this result, which will be 00010 and this will be negative number, i.e., -00010, which is the answer.
Case-3: Addition of two negative numbers:
You need to take 1’s complement for both numbers, then add these 1’s complement of numbers. Since there will always be end-around carry bit, so add this again to the MSB of result. Now, take 1’s complement also of previous result, so this will be negative number.
Alternatively, you can add both negative number directly, and get this result which will be negative only.
Example: add -1010 and -0101 in five bit-register.
These five bit numbers are -01010 and -00101. Add complements of these numbers, 10101+11010 =1 01111 . Since, there is a carry bit 1, so add this to the LSB of result, i.e., 01111+1=10000 . Now take the 1’s complement of this result, which will be 01111 and this number is negative, i.e, -01111, which is answer.
Note that end-around-carry-bit addition occurs only in 1’s complement arithmetic operations but not in 2’s complement arithmetic operations.

