Number of triangles in a plane if no more than two points are collinear

Let us see how to calculate the number of triangles in a plane with n number of points given, with the constraint that not more than two points are collinear.

Computing the number of triangles in a plane with no more than two collinear points is a typical problem in computational geometry, and it is used in computer graphics, image processing, and other areas of computer science.

While creating a 2D image from a 3D scene in 3D graphics, for instance, the issue of counting triangles in a plane with no more than two points collinear can come up. The triangle counting procedure can be used to determine how many triangles are present in the final 2D image after projecting the 3D scene onto a plane in this situation. The complexity of the scene can be ascertained with this, and rendering speed can be improved.

In image processing, where we might want to count the number of unique objects or shapes in an image, this problem comes helpful. In this instance, we can represent the image as a collection of points on a plane, and then we can count the number of triangles that can be created between these points by applying the triangle counting technique. We may determine the approximate number of distinct items or shapes in the image by counting how many triangles are formed.

Explanation

Let’s understand the problem with a few examples and try to solve it.

The aim is to determine how many triangles are formed in a plane with n points such that no more than two points are collinear.

Example −

Suppose N is the number of points in a plane.

N = 3

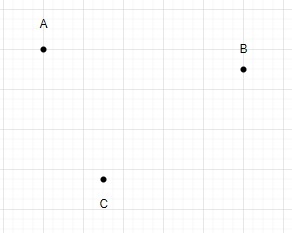
We can draw only one triangle using these points.

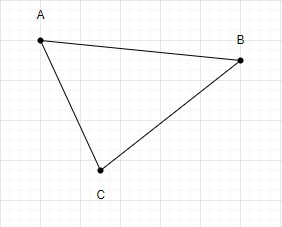
So, the total number of triangles made using 3 points is 1.

Let’s N = 4

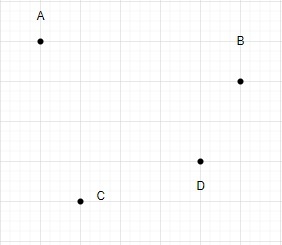
Let’s draw triangles using these four points.

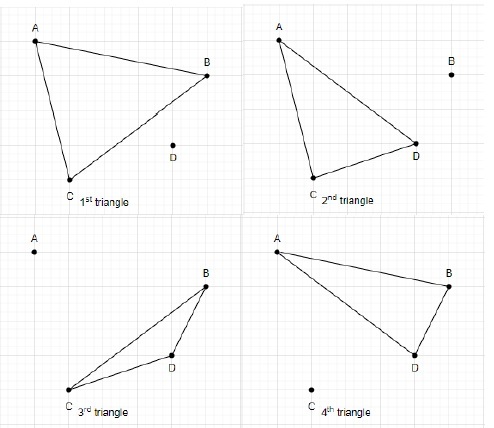
The total number of triangles formed using 4 points is 4.

Let’s see some mathematics involved in calculating the number of triangles. This can be obtained using Permutations and Combinations. To construct a triangle 3 points are needed at a time from the total number of points.

So, if a plane contains n points and no more than two of them are collinear, then the number of triangles in the plane is given by the formula.

$$\mathrm{n_{C_{3}}\:=\:\frac{n(n-1)\:(n-2)}{6}}$$

Approach

Program to find the number of triangles in a plane if no more than two points are collinear uses the following Algorithm.

• Take the number of points in a plane as input with constraints not more than two of them are collinear.

• Calculate the total number of triangles using the above-mentioned formula.

• Print the total number of triangles as output.

Example

C++ program to find the number of triangles in a plane if no more than two points are collinear.

#include <iostream>
using namespace std;

int main() {
   int number_of_points = 4;
   int number_of_triangle;
   
   number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
   cout << "Total number of triangles formed using " << number_of_points<< " points = " <<  number_of_triangle << endl;
   
   return 0;
}

Output

Total number of triangles formed using 4 points = 4

Complexities

Time complexity: O(1), As this code performs a fixed number of calculations, regardless of the size of the input.

Space complexity: O(1), As the code uses a fixed number of variables to store input values and results, regardless of the size of the input.

Conclusion

In this article, we have tried to explain the approach to find the total number of possible triangles with n given points, with the constraint that no two points are collinear. I hope this article helps you to learn the concept in a better way.