Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count of triangles with total n points with m collinear in C++
We are given two variables n and m representing the number of points on a 2D plane. Out of n points, m points are collinear. The goal is to find the number of triangles that can be formed using these n points.
Collinear points − The points that lie on the same line are called collinear. Points A and B are collinear.
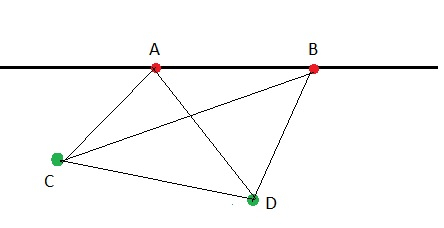
Given n=4 (A,B,C,D ) , m=2 (A,B)
Number of triangles −
Choosing any three points out of 4 = 4C3
But collinear points cannot form triangle so remove possible triangles that will be counted above = 2C3
Total triangles= 4C3 - 2C3= 4-0 = 4 ( ABC, ACD, BCD, ABD )
For n and m = nC3 - mC3
Let us understand with examples.
Input − n=5, m=3
Output − Count of triangles with total n points with m collinear are − 9
Explanation − Total triangles = 5C3 - 3C3 = 10 - 1 = 9
Input − n=10, m=5
Output − Count of triangles with total n points with m collinear are − 110
Explanation − Total triangles = 10C3 - 5C3 = 120 - 10 = 110
Approach used in the below program is as follows
We will create a pascal triangle for containing calculations of combinations. Every row is calculated using addition of previous row columns.
Take variables n and m as input for a number of points.
Function collinear_points(int n,int m) takes n and m and returns the count of triangles with total n points with m collinear.
Set count = check(n, 3) - check(m, 3); ( for calculating nC3 - mC3 )
Function check(int n, int r) takes n and r and returns value of nCr
Take an array arr of length r+1.
Set the whole array with 0’s using memset.
Set arr[0] = 1.
Using two for loops from i=0 to i<=n. And j=min (i,r) to j>0 calculate the pascal triangle as arr[j]=arr[j]+arr[j-1].
In the end we will get arr[r] as nCr. Return it.
After the end of function check(). We will get count of triangles
Return count as result.
Example
#include <bits/stdc++.h>
using namespace std;
int check(int n, int r){
int arr[r+1];
memset(arr, 0, sizeof(arr));
arr[0] = 1;
for (int i = 1; i <= n; i++){
for (int j = min(i, r); j > 0; j--){
arr[j] = arr[j] + arr[j-1];
}
}
return arr[r];
}
int collinear_points(int n,int m){
int count = check(n, 3) - check(m, 3);
return count;
}
int main(){
int n = 6, m = 2;
cout<<"Count of triangles with total n points with m collinear are: "<< collinear_points(n, m);
return 0;
}Output
If we run the above code it will generate the following output −
Count of triangles with total n points with m collinear are: 20
88 Views
