
- NGN - Home
- NGN - Pulse Code Modulation
- NGN - Multiplexing
- NGN - Frame Structure
- NGN - Higher Order Multiplexing
- Plesiochronous Digital Hierarchy
- NGN - Synchronous Digital Hierarchy
- NGN - WDM Technology
- Micro Electro Mechanical Systems
- NGN - Varieties Of WDM
NGN - Pulse Code Modulation
The advent of high-speed voice and data communications has brought about the need for a fast medium for transporting the information. Digital circuits or links have evolved from the need to transmit voice or data in digital form.
The conversion from analogue to digital form follows a four-stage processes (see the following Figure) and will be detailed in the following sections.

Sampling
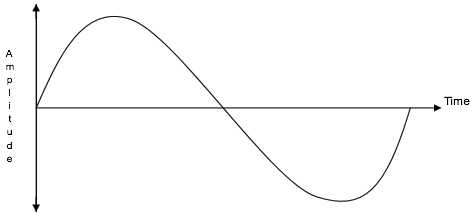
Voice frequencies take the form of an analogue signal i.e. sine wave (see the following Figure). This signal has to be converted into a binary form for it to be carried over a digital medium. The first stage of this conversion is to convert the audio signal into a Pulse Amplitude Modulation(PAM) signal. This process is generically known as sampling.
The sampling process must gather sufficient information from the incoming voice frequencies to enable a copy of the original signal to be made. Voice frequencies are normally in the range of 300Hz to 3400Hz, typically known as the commercial speech band.
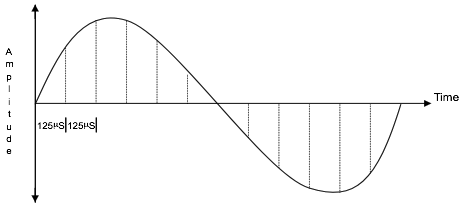
To obtain a sample, a sampling frequency is applied to the original voice frequency. The sampling frequency is determined by the Nyquist Sampling Theorem, which dictates that the frequency of sampling should be at least twice the highest frequency component.
This ensures that a sample is taken a minimum of once in each half cycle, thus, eliminating the possibility of sampling at zero points of the cycle, which would have no amplitude. This results into the sampling frequency being a minimum of 6.8 KHz.
The European standard samples an incoming signal at 8 KHZ, ensuring a sample, is taken every 125micro seconds or 1/8000th of a second (see the following Figure).
Quantization
The amplitude of each sample would ideally be assigned a binary code (1s or 0s), but as there can be an infinite number of amplitudes; therefore, there need to be an infinite number of binary codes available. This would be impractical, so another process has to be employed, which is known as quantizing.
Quantizing compares the PAM signal against a quantizing scale, which has a finite number of discrete levels. The quantizing scale splits into 256 quantizing levels, of which, 128 are positive levels and 128 are negative levels.
The quantization stage involves allocating a unique 8 bit binary code appropriate to the quantizing interval into which the amplitude of the PAM signal falls (see the following Figure).
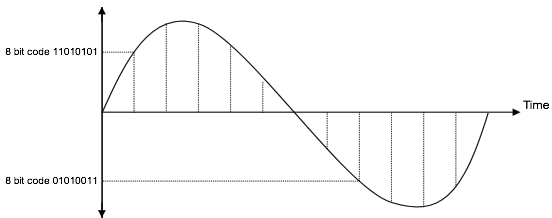
This comprises of 1 polarity bit with the remaining 7 bits used to identify the quantization level (as shown in the above figure).
The first bit as seen before is the polarity bit, the next three bits for the segment code, giving eight segment codes, and the remaining four bits for the quantization level, giving sixteen quantization levels.
Companding
The quantizing process itself leads to a phenomenon known as quantization distortion. This occurs when the sampled signal amplitude falls between the quantization levels. The signal is always rounded up to the nearest whole level. This difference between the sampled level and the quantizing level is quantizing distortion.
The rate of change of the amplitude of a signal varies at different parts of the cycle. This happens most at high frequencies as the amplitude of the signal changes faster than at the low frequencies. To overcome this, the first segment code has the quantization levels close together. The next segment code is then double the height of the previous and so on. This process is known as companding, as it compresses larger signals and expands smaller signals.

In Europe they use the A-law of companding, compared to North America and Japan who use the law.
As quantization distortion is equivalent to noise, companding improves the signal to noise ratio on low amplitude signals, and produces an acceptable signal to noise ratio over the complete range of amplitudes.
Encoding
In order for the binary information to be transmitted over a digital path, the information has to be modified into a suitable line code. The encoding technique employed in Europe is known as High Density Bipolar 3 (HDB3).
HDB3 is derived from a line code called AMI or Alternate Mark Inversion. Within AMI encoding, there are 3 values used: no signal to represent a binary 0, and a positive or negative signal that is used alternately to represent a binary 1.
One problem associated with AMI encoding occurs when a long string of zeros are transmitted. This can cause phase lock loop problems at the distant end receiver.
HDB3 works in a similar way to AMI, but incorporates an extra encoding step that replaces any string of four zeros by three zeros followed by a 'violation bit. This violation is of the same polarity of the previous transition (see the following Figure).

As can be seen in the example, 000V replaces the first string of four zeros. However, using this type of encoding could lead to a mean D.C. level being introduced into the signal, as a long string of zeros could be present, all being encoded in the same way. To avoid this, the encoding of each successive four zeros is changed to B00V, by using a 'Bipolar violation' bit that alternates in polarity.
From this, it can be assumed that with HDB3 encoding, the maximum number of zeros without a transition is three. This encoding technique is often referred as the modulation format.