Addition of Two n-Bit Binary Numbers

In digital electronics and digital systems such as digital computers, calculator, etc., the binary numbers and their arithmetic operations play a vital role. Just like the decimal number system, we can perform all the four basic arithmetic operations, i.e. addition, subtraction, multiplication, and division of binary numbers as well. Read this article to learn how you can add two n-bit binary numbers.

What is Binary Addition?

Binary addition is a basic arithmetic operation performed on binary numbers in which two binary number of any digit are added to obtain a sum.

As we know, a binary number system has base two, and consists of only two symbols or digits, i.e. 0 and 1. Thus, the addition of two binary number is similar to that of the decimal numbers, except the base of the system is 2. Before discussion the process of binary addition, let us get the idea about the rules of binary addition.

Rules of Binary Addition

We have to follow certain rules of Boolean algebra to perform the binary addition of two binary numbers. There are four rules to be followed to perform the binary addition. These rules are given as follows −

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 0 (Carry 1)

Hence, when first three sets of bits are added, there is no carry generated. But, when two 1-bits are added, the sum bit is 0 and a carry bit 1 is produced.

Now, let us understand the addition of two binary numbers with the help of examples.

Example

Add the two 3-bit binary numbers 111 and 101.

Solution

Given binary numbers are, 111 and 101. We can add these two 3-bit binary numbers are follows −

	3rd Column	2nd Column	1st Column
Carry from previous addition	1	1	No carry
First Binary Number	1	1	1
Second Binary Number	1	0	1
Sum bits	1	0	0
Carry Bits	1	1	1

Therefore, the result of this binary addition is,

111 + 101 = 1100

The systematic representation of this binary addition is shown in Figure-1.

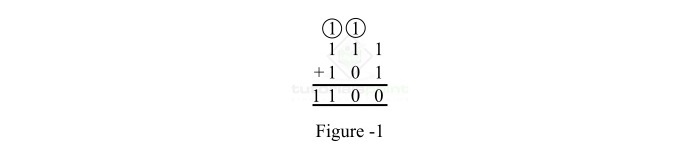
Explanation

The binary addition of binary numbers 111 and 101 is performed as per the following steps −

• Step 1 − Firstly, we consider the 1^st column, and add the bits of first column, i.e. (1+1), it gives the sum bit 0, and carry bit 1 as per the rules of binary addition. The sum bit is left in the 1^st column and the carry bit 1 is forward to the 2^nd column.

• Step 2 − In the 2^nd column, we add 1+(1+0). It gives the sum bit 0 (leave in the 2^nd column) and carry bit 1 which is forwarded to the next column.

• Step 3 − In the 3^rd column, we add 1+(1+1). It gives the sum bit 1 and a carry bit 1.

Finally, record the sum result which is 1100.

After understanding the binary addition for a certain number of bits, we can extend it to any number of bits.

Addition of Two n-Bit Binary Numbers

The procedure of binary addition followed in the above example can be generalized to any two binary numbers of n-bits.

We can perform the addition of two n-bit binary numbers as per the following steps −

Let there are two binary numbers of n-bit as,

$$A=A_{n}\cdot \cdot \cdot A_{3}A_{2}A_{1}$$

$$B=B_{n}\cdot \cdot \cdot B_{3}B_{2}B_{1}$$

Now, let’s add these two binary numbers.

	nth Column	3rd Column	2nd Column	1st Column
Carry from previous addition	C(n-1)	C2	C1	No Carry
First Binary Number	An	A3	A2	A1
Second Binary Number	Bn	B3	B2	B1
Sum bits	Sn = An + Bn + C(n-1)	S3 = A3 + B3 + C2	S2 = A2 + B2 + C1	S1 = A1 + B1
Carry Bits	Cn	C3	C2	C1

The result of this binary addition of these two n-bit binary numbers will be,

$$S=C_{n}S_{n}\cdot \cdot \cdot S_{3}S_{2}S_{1}$$

This addition can also be represented in the standard layout as shown in Figure-2.

Explanation − This binary addition of two n-bit binary numbers is performed as per the following steps −

• Step 1 − Firstly, consider the 1^st column, and add the bits of 1^st column, i.e. (A₁ + B₁). It gives the sum bit S₁ and carry bit C₁ as a result.

• Step 2 − Leave the sum bit S₁ in the 1^st column and forward the carry bit C₁ to the 2^nd column.

• Step 3 − Now, add bits of 2^nd column, i.e. (C₁ + A₂ + B₂). It gives a sum bit S₂ and a carry bit C2. Leave the sum bit S₂ in the 2^nd column and move the carry bit to the 3^rd column.

• Step 4 − Perform the addition for each column in the same way.

• Step 5 − In the n^th column, we add (C_(n-1) + A_n + B_n). It gives a sum bit S_n and carry bit C_n.

Finally, record all the result bits together to obtain the sum of the given n-bit binary numbers as follows −

$$S=C_{\left ( n-1 \right )}S_{n}\cdot \cdot \cdot S_{3}S_{2}S_{1}$$

This is the resultant sum of the addition of two n-bit binary numbers.

This is all about the addition of two n-bit binary numbers. In order to excel in the addition of binary number, try to solve the following tutorial problems.

Q. 1 − Add the two 5-bit binary numbers 11011 and 10110.

Q. 2 − Add the two binary numbers: 1011 + 1101.

Q. 3 − Add the two binary numbers 1110011 and 1011011.

Q. 4 − Perform the addition: 10111 + 10011.

Q. 5 − Add these two binary numbers: 1111 + 1001.