Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
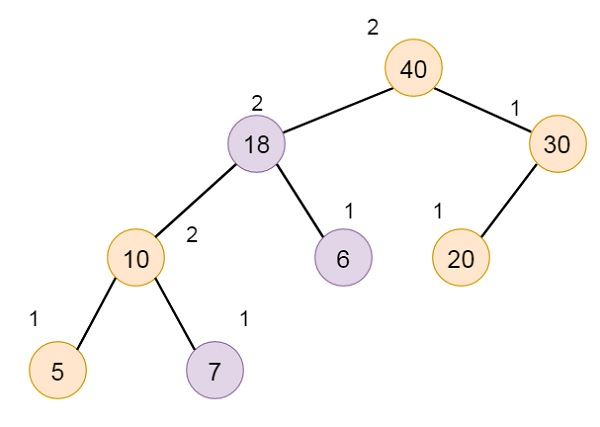
Melding Two Max HBLTs in Data Structure
The meld strategy is done easily using recursion. Suppose A and B are two HBLTs, that will be melded. If one of them is empty, then simply make another one as final result. If no empty HBLT is there, then we have to compare the elements in the two roots. The root with larger element becomes the root of melded HBLT.
Suppose A has larger root. And that is its left subtree is L. Suppose C be the max HBLT, that results from melding the right subtree of A and the HBLT B. The final HBLT will have A as root, and L and C as its subtrees. If s value of L is smaller than that of C, then C is basically the left subtree. Otherwise L will be left subtree.
Suppose we have two elements like −
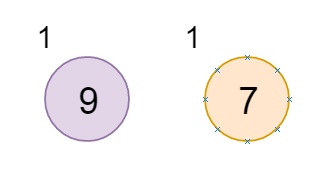
We want to meld them. (The node is holding the value, the number outside of the node are s values for the corresponding node.)
Now let us see how to meld. Suppose 7 is added as right child of 9, but here, s(L) of 9 is 0, and s(R) of 9 is 1, so they will be swapped, and 7 will be its right child.
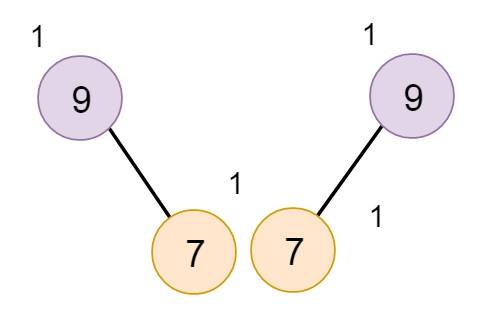
Another Example −
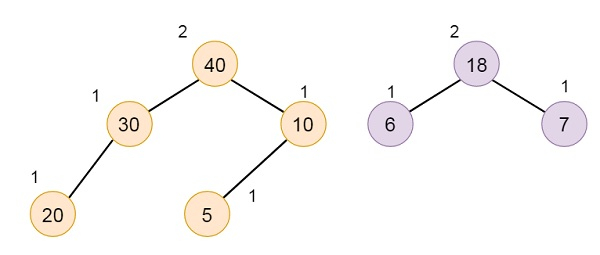
Temporarily add the smaller HBLT as right of the larger one.
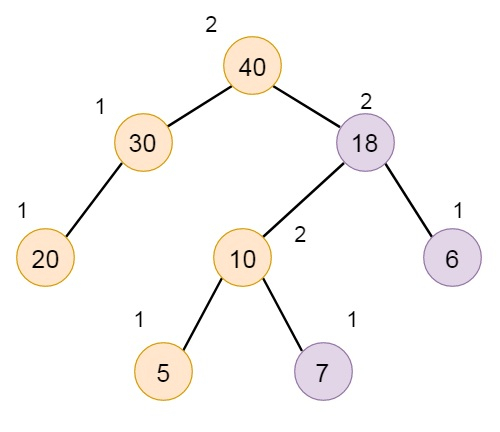
This is not maintaining the property of HBLT,
180 Views
