- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum Possible Edge Disjoint Spanning Tree From a Complete Graph in C++
Suppose we have a complete graph; we have to count number of Edge Disjoint Spanning trees. The Edge Disjoint Spanning trees are spanning trees, where no two trees in the set have an edge in common. Suppose the N (number of vertices) is 4, then output will be 2. The complete graph using 4 vertices is like below −
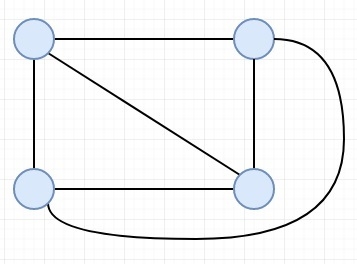
Two edge disjoint spanning trees are like −
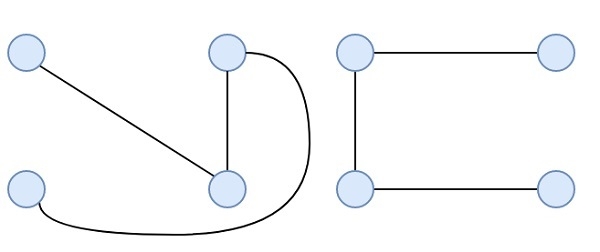
The maximum number of edge disjoint spanning tree from a complete graph, with N vertices will be $[\frac{n}{2}]$
Example
#include <iostream>
#include <cmath>
using namespace std;
int maxEdgeDisjointSpanningTree(int n){
return floor(n/2);
}
int main() {
int n = 4;
cout << "Maximum Edge Disjoint Spanning Tree: " <<
maxEdgeDisjointSpanningTree(n);
}Output
Maximum Edge Disjoint Spanning Tree: 2
Published on 21-Oct-2019 12:21:43
- Related Questions & Answers
- C++ Program to Perform Edge Coloring on Complete Graph
- C++ Program to Find Maximum Number of Edge Disjoint Paths
- Maximum edge removal from tree to make even forest in C++
- Spanning Tree Protocol
- Program to Find Out if an Edge is a Part of a Minimum Spanning Tree in Python
- Mininum spanning tree algorithms
- Count Complete Tree Nodes in C++
- Complete Binary Tree Inserter in C++
- C++ Program to Perform Edge Coloring of a Graph
- Complete Graph Class in Javascript
- Minimum spanning tree (MST) in Javascript
- Minimum Spanning Tree in Data Structures
- Finding the number of spanning trees in a graph
- C++ Program to Find the Edge Connectivity of a Graph
- C++ program to Calculate the Edge Cover of a Graph
Advertisements