Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum edge removal from tree to make even forest in C++
Problem statement
Given an undirected tree which has even number of vertices, we need to remove the maximum number of edges from this tree such that each connected component of the resultant forest has an even number of vertices.
Example
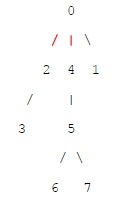
In above shown tree, we can remove at max 2 edges 0-2 and 0-4 shown in red such that each connected component will have even number of vertices.
Algorithm
- Do DFS from any starting node as tree is connected
- Initialize count of nodes in subtree rooted under current node as 0
- Do following recursively for every subtree of current node −
- If size of current subtree is even, increment result by 1 as we can disconnect the subtree
- Else add count of nodes in current subtree to current count
Example
Let us now see an example −
#include <bits/stdc++.h>
using namespace std;
int dfs(vector<int> g[], int u, bool visit[], int& res) {
visit[u] = true;
int currComponentNode = 0;
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if (!visit[v]) {
int subtreeNodeCount = dfs(g, v, visit, res);
if (subtreeNodeCount % 2 == 0)
res++;
else
currComponentNode += subtreeNodeCount;
}
}
return (currComponentNode + 1);
}
int maxEdgeRemovalToMakeForestEven(vector<int> g[], int N) {
bool visit[N + 1];
for (int i = 0; i <= N; i++)
visit[i] = false;
int res = 0;
dfs(g, 0, visit, res);
return res;
}
void addEdge(vector<int> g[], int u, int v) {
g[u].push_back(v);
g[v].push_back(u);
}
int main() {
int edges[][2] = {{0, 2}, {0, 1}, {0, 4}, {2, 3}, {4, 5}, {5, 6}, {5, 7} };
int N = sizeof(edges)/sizeof(edges[0]); vector<int> g[N + 1];
for (int i = 0; i < N; i++)
addEdge(g, edges[i][0], edges[i][1]);
cout << "Answer = " << maxEdgeRemovalToMakeForestEven(g, N) << endl;
return 0;
}Output
Answer = 2
Updated on: 31-Dec-2019
268 Views
Advertisements