Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum length cycle that can be formed by joining two nodes of a binary tree in C++
We are given a binary tree. The goal is to find the maximum length cycle in the given tree. We will do this by finding the maximum height of the left subtree and right subtree from the root node and will join these maximum length paths to get the longest cycle.
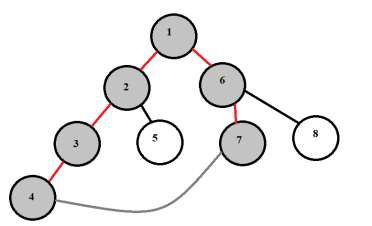
For the above tree the maximum length cycle is 1-2-3-4-7-6 or 1-6-7-4-3-2-1. The length is 6.
Input − tree
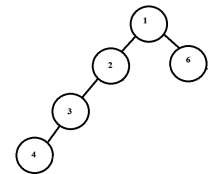
Output − Maximum length cycle is − 5
Explanation − The max height of left subtree is 3 and of right subtree is 1. Cycle length becomes 3+1+1=5. Cycle is 1-2-3-4-6 or 1-6-4-3-2
Input − tree
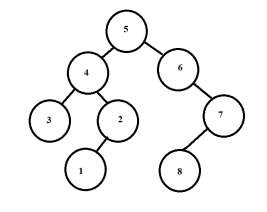
Output − Maximum length cycle is − 7
Explanation − The max height of left subtree is 3 and of right subtree is 3. Cycle length becomes 3+3+1=7. Cycle is 5-4-2-1-8-7-6 or 5-6-7-8-1-2-4-5
Approach used in the below program is as follows
Create a class treenode which has public data members − int data for weight of the node, left and right treenode pointers to point to other such nodes.
Function newNode(int data) takes data as a parameter and creates a node with left and right pointers as NULL.
Create a tree by calling newnode() function.
Function maxheight(treenode* root) takes a root of the tree and returns the maximum height of the tree rooted at root.
This function checks if the root is NULL , means height is 0, return 0.
lheight and rheight calculates the heights of left and right subtree of node root, by recursive calls to maxheight(root->left); and maxheight(root->right);
Return the maximum value obtained by comparing lheight and rheight.
Inside main we store values of maximum height of left subtree and right subtree of tree Node.
Now the maximum length cycle is the sum of both maxlheight +maxrheight+1 for including the root itself.
Print the length of the cycle as a result.
Example
#include <bits/stdc++.h>
using namespace std;
//class for tree
class treenode{
public:
int data;
treenode* left;
treenode* right;
};
//find maximum height between left and right subtree of current root
int maxheight(treenode* root){
if (root == NULL)
return 0;
else{
int lheight = maxheight(root->left);
int rheight = maxheight(root->right);
//find maximum height
if (lheight > rheight)
return(lheight + 1);
else
return(rheight + 1);
}
}
//creating a node of tree
treenode* newNode(int data){
treenode* Node = new treenode();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return(Node);
}
int main(){
treenode *root = newNode(6);
root->left = newNode(8);
root->right = newNode(9);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->left->right->right = newNode(7);
root->left->right->right->left = newNode(2);
int maxlheight=maxheight(root->left);
int maxrheight=maxheight(root->right);
int maxlheight=maxDepth(root->left);
int maxrheight=maxDepth(root->right);
cout << "Maximum length cycle: " << maxlheight+maxrheight+1;
return 0;
}Output
Maximum length cycle: 6
160 Views
