Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum Consecutive Increasing Path Length in Binary Tree in C++
Suppose we have a binary tree; we have to calculate the length of the longest path which consists of nodes with consecutive values in increasing order. Every node will be treated as a path of length 1.
So, if the input is like
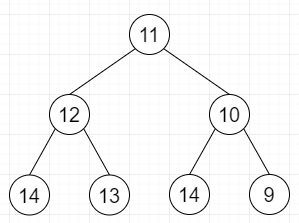
then the output will be 3 as (11, 12, 13) is maximum consecutive path.
To solve this, we will follow these steps −
- Define a function solve(), this will take root, prev_data, prev_length,
- if not root is non-zero, then −
- return prev_length
- cur_data := val of root
- if cur_data is same as prev_data + 1, then −
- return maximum of solve(left of root, cur_data, prev_length+1) and solve(right of root, cur_data, prev_length+1)
- newPathLen := maximum of solve(left of root, cur_data, 1) and solve(right of root, cur_data, 1)
- return maximum of prev_length and newPathLen
- From the main method do the following −
- if root is same as NULL, then −
- return 0
- return solve(root, val of root-1, 0)
Example (C++)
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
class TreeNode {
public:
int val;
TreeNode *left, *right;
TreeNode(int data) {
val = data;
left = NULL;
right = NULL;
}
};
int solve(TreeNode *root, int prev_data, int prev_length){
if (!root)
return prev_length;
int cur_data = root->val;
if (cur_data == prev_data+1){
return max(solve(root->left, cur_data, prev_length+1), solve(root->right, cur_data, prev_length+1));
}
int newPathLen = max(solve(root->left, cur_data, 1), solve(root->right, cur_data, 1));
return max(prev_length, newPathLen);
}
int maxLen(TreeNode *root){
if (root == NULL)
return 0;
return solve(root, root->val-1, 0);
}
int main(){
TreeNode *root = new TreeNode(10);
root->left = new TreeNode(11);
root->right = new TreeNode(9);
root->left->left = new TreeNode(13);
root->left->right = new TreeNode(12);
root->right->left = new TreeNode(13);
root->right->right = new TreeNode(8);
cout << maxLen(root);
return 0;
}Input
TreeNode *root = new TreeNode(10); root->left = new TreeNode(11); root->right = new TreeNode(9); root->left->left = new TreeNode(13); root->left->right = new TreeNode(12); root->right->left = new TreeNode(13); root->right->right = new TreeNode(8);
Output
3
Updated on: 27-Aug-2020
159 Views
Advertisements