Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum sum of nodes in Binary tree such that no two are adjacent using Dynamic Programming in C++ program
In this problem, we are given a Binary Tree with each node having a value. Our task is to create a program to find the Maximum sum of nodes in Binary tree such that no two are adjacent using Dynamic Programming.
Problem Description − We will be choosing the subsets of the binary tree to make the sum maximum in such a way that the nodes are not connected directly.
Let’s take an example to understand the problem,
Input
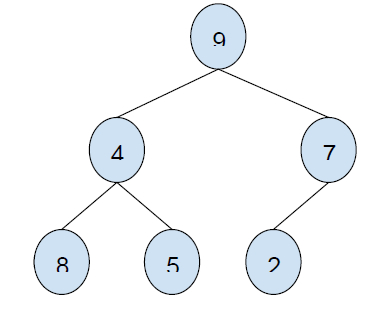
Output
24
Explanation
Elements to be taken under consideration are: 8 + 5 + 9 + 2 = 24
Solution Approach
A solution to the problem is by using a map and finding the sum of nodes such that they form maxSum. Both nodes and their children cannot be
considered for the sum according to the condition given. So, we need to check the fact that before considering a node, we need to check if its child tree has some elements that constitute a greater sum.
Finding the sum of the same parent−child subtree multiple times for each node will increase computation overhead and in order to deal with it, we will use memorization and store the maxSum till the node in a map which can be used later on.
Example
Program to illustrate the working of our solution,
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
struct node *left, *right;
};
struct node* newNode(int data){
struct node *temp = new struct node;
temp−>data = data;
temp−>left = temp−>right = NULL;
return temp;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum);
int sumSubTreeNodes(node* node, map<struct node*, int>& nodeSum){
int maxSum = 0;
if (node−>left)
maxSum += findMaxSumBT(node−>left−>left, nodeSum) +
findMaxSumBT(node−>left−>right, nodeSum);
if (node−>right)
maxSum += findMaxSumBT(node−>right−>left, nodeSum) +
findMaxSumBT(node−>right−>right, nodeSum);
return maxSum;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum){
if (node == NULL)
return 0;
if (nodeSum.find(node) != nodeSum.end())
return nodeSum[node];
int sumInclCurr = node−>data + sumSubTreeNodes(node, nodeSum);
int sumExclCurr = findMaxSumBT(node−>left, nodeSum) +
findMaxSumBT(node−>right, nodeSum);
nodeSum[node] = max(sumInclCurr, sumExclCurr);
return nodeSum[node];
}
int main(){
node* root = newNode(9);
root−>left = newNode(4);
root−>right = newNode(7);
root−>left−>left = newNode(8);
root−>left−>right = newNode(5);
root−>right−>left = newNode(2);
map<struct node*, int> nodeSum;
cout<<"Maximum sum of nodes in Binary tree such that no two are
adjacent using Dynamic Programming is "<<findMaxSumBT(root,
nodeSum);
return 0;
}Output
Maximum sum of nodes in Binary tree such that no two are adjacent using Dynamic Programming is 24
269 Views
To Continue Learning Please Login