Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Implementing K-means clustering with SciPy by splitting random data in 3 clusters?
Yes, we can also implement a K-means clustering algorithm by splitting the random data in 3 clusters. Let us understand with the example below −
Example
#importing the required Python libraries:
import numpy as np
from numpy import vstack,array
from numpy.random import rand
from scipy.cluster.vq import whiten, kmeans, vq
from pylab import plot,show
#Random data generation:
data = vstack((rand(200,2) + array([.5,.5]),rand(150,2)))
#Normalizing the data:
data = whiten(data)
# computing K-Means with K = 3 (3 clusters)
centroids, mean_value = kmeans(data, 3)
print("Code book :
", centroids, "
")
print("Mean of Euclidean distances :", mean_value.round(4))
# mapping the centroids
clusters, _ = vq(data, centroids)
print("Cluster index :", clusters, "
")
#Plotting using numpy's logical indexing
plot(data[clusters==0,0],data[clusters==0,1],'ob',
data[clusters==1,0],data[clusters==1,1],'or',
data[clusters==2,0],data[clusters==2,1],'og')
plot(centroids[:,0],centroids[:,1],'sg',markersize=8)
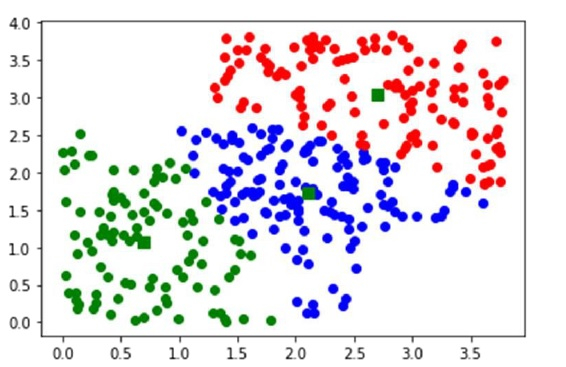
show()Output
Code book : [[2.10418081 1.73089074] [2.69953885 3.04708713] [0.6994524 1.06646081]] Mean of Euclidean distances : 0.7661 Cluster index : [1 1 0 1 1 1 1 0 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 0 1 0 1 0 1 0 0 0 0 0 1 0 1 1 0 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 1 1 0 1 1 0 1 0 1 1 0 0 0 1 1 0 0 0 1 0 1 0 1 1 1 0 0 1 0 1 0 1 1 0 1 1 0 1 0 0 0 1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 0 0 1 1 1 0 1 1 1 1 1 0 1 0 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 0 1 0 1 1 0 0 1 1 0 0 0 1 1 0 1 1 1 1 0 1 0 0 1 1 1 1 2 2 0 0 2 2 2 2 0 2 2 2 2 2 2 2 2 0 0 0 0 2 2 2 2 2 0 2 2 2 0 2 2 0 2 0 0 2 2 0 0 0 0 2 2 2 0 2 2 0 2 0 2 0 0 2 0 2 2 0 2 2 2 0 0 2 2 2 2 2 2 0 2 2 2 2 2 0 0 2 2 2 2 0 2 2 2 0 2 0 2 0 2 2 2 0 0 0 0 2 2 2 0 2 2 2 2 2 0 2 2 2 0 2 2 0 2 1 2 0 2 2 2 0 2 2 0 0 0 2 0 0 0 0 2 2 2 0 2 2 2 2 0 2 2 2 2 0 0 2]
Updated on: 14-Dec-2021
139 Views
Advertisements