Analyzing Decision Tree and K-means Clustering using Iris dataset

Decision trees and K-means clustering algorithms are popular techniques used in data science and machine learning to uncover patterns and insights from large datasets like the iris dataset. As we all know, Artificial Intelligence is employed extensively in our daily lives, from reading the news on a mobile device to analyzing complicated data at work. AI has improved the speed, accuracy, and efficiency of human endeavors. AI developments have enabled us to do things that were previously deemed impossible.

Here in this article, we will learn about the decision tree algorithm and k means clustering algorithm and how to apply the decision tree algorithm and k means clustering algorithm on the iris dataset

Iris dataset

The Fisher's Iris data set is a multivariate data set made famous by the British statistician and biologist Ronald Fisher in his 1936 work The use of numerous measurements in taxonomic issues as an example of linear discriminant analysis. Fisher's work was published in the journal. Edgar Anderson collected the data in order to investigate the morphological differences that exist between the blooms of three closely related species of iris. On the Gaspé Peninsula, two of the three species were collected "all from the same pasture, on the same day, by the same person using the same measurement equipment."

The dataset consists of 50 specimens collected from each of the three species of Iris (Iris setosa, Iris virginica, and Iris versicolor). The length and width of the sepals and petals were measured in centimeters for each individual sample. These are two of the four features that were measured.

Decision tree

Applications that include classification and regression often make use of a method known as a decision tree, which is a non-parametric form of supervised learning. It has a hierarchical structure that looks like a tree and is comprised of a root node, branches, internal nodes, and leaf nodes.

K-means clustering

k-means clustering is a technique of vector quantization that has its roots in the field of signal processing. Its goal is to divide n observations into k clusters so that each observation belongs to the cluster with the closest mean (cluster centers or cluster centroid), which acts as the prototype for the cluster. This leads to the data space being divided up into Voronoi cells as a consequence. While the geometric median is the only one that can minimize Euclidean distances, the mean is optimized for squared errors. It is possible, for instance, to locate improved Euclidean solutions by making use of k-medians and k-medoids.

Decision tree and k-means clustering algorithm on iris dataset

Example

import pandas as pdd
from sklearn import datasets
import numpy as npp
import sklearn.metrics as smm
import matplotlib.patches as mpatchess
from sklearn.cluster import KMeans
import matplotlib.pyplot as pltt
from sklearn.metrics import accuracy_score
%matplotlib inline
iris = datasets.load_iris()
print(iris.target_names)
print(iris.target)
x1 = pdd.DataFrame(iris.data, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal Width'])
y1 = pdd.DataFrame(iris.target, columns=['Target'])
x1.head()

Output

['setosa' 'versicolor' 'virginica']

 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

     Sepal Length  Sepal Width  Petal Length Petal Width
0   5.1        3.5                   1.4                0.2
1   4.9        3.0                 1.4                0.2
2   4.7        3.2                   1.3                0.2
3   4.6        3.1                   1.5                0.2
4   5.0        3.6                   1.4                0.2

Print the first 5 rows of the target variable which is y −

y1.head()

Output

   Target
0   0
1   0
2   0
3   0
4   0

In the next step, plot the figure for the dataset which shows the difference between the variables of the dataset −

pltt.figure(figsize=(12,3))
colors = npp.array(['red', 'green', 'blue'])
iris_targets_legend = npp.array(iris.target_names)
red_patch = mpatchess.Patch(color='red', label='Setosa')
green_patch = mpatchess.Patch(color='green', label='Versicolor')
blue_patch = mpatchess.Patch(color='blue', label='Virginica')
pltt.subplot(1, 2, 1)
pltt.scatter(x1['Sepal Length'], x1['Sepal Width'], c=colors[y1['Target']])
pltt.title('Sepal Length vs Sepal Width')

pltt.legend(handles=[red_patch, green_patch, blue_patch])

pltt.subplot(1,2,2)

pltt.scatter(x1['Petal Length'], x1['Petal Width'], c= colors[y1['Target']])
pltt.title('Petal Length vs Petal Width')
pltt.legend(handles=[red_patch, green_patch, blue_patch])

Output

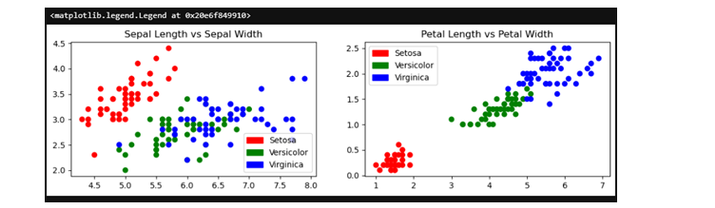
We will define clusters in the next step

iris_k_mean_model = KMeans(n_clusters=3)
iris_k_mean_model.fit(x1)
print(iris_k_mean_model.labels_)

Output

KMeans(n_clusters=3)
[[5.9016129  2.7483871  4.39354839 1.43387097]
 [5.006      3.428      1.462      0.246     ]
 [6.85       3.07368421 5.74210526 2.07105263]]

Now, we will plot the figure before and after classification −

pltt.figure(figsize=(12,3))

colors = npp.array(['red', 'green', 'blue'])

predictedY = npp.choose(iris_k_mean_model.labels_, [1, 0, 2]).astype(npp.int64)

pltt.subplot(1, 2, 1)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c=colors[y1['Target']])
pltt.title('Before classification')
pltt.legend(handles=[red_patch, green_patch, blue_patch])

pltt.subplot(1, 2, 2)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c=colors[predictedY])
pltt.title("Model's classification")
pltt.legend(handles=[red_patch, green_patch, blue_patch])

Output

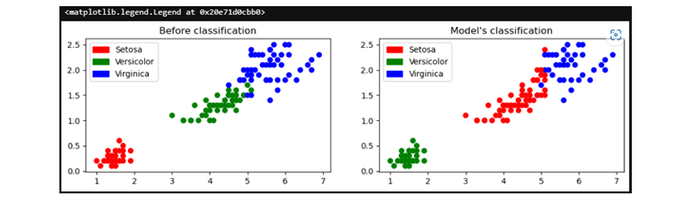
Next, we will print the accuracy of the model −

smm.accuracy_score(predictedY, y1['Target'])

Output

0.24

Next, we will test the model and print the accuracy for the test dataset and the train dataset −

from sklearn.metrics import accuracy_score

X = iris.data

# Extracting Target / Class Labels
y = iris.target

# Import Library for splitting data
from sklearn.model_selection import train_test_split

# Creating Train and Test datasets
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state = 50, test_size = 0.25)

# Creating Decision Tree Classifier
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()

clf.fit(X_train,y_train)
# Predict Accuracy Score
y_pred = clf.predict(X_test)
print("Train data accuracy:",accuracy_score(y_true = y_train, y_pred=clf.predict(X_train)))
print("Test data accuracy:",accuracy_score(y_true = y_test, y_pred=y_pred))

Output

Train data accuracy: 1.0
Test data accuracy: 0.9473684210526315

Conclusion

In conclusion, the iris dataset is a conventional machine-learning dataset that is often used to test different algorithms. Here, we used the popular decision tree algorithm and the K-means clustering algorithm to look at the data.

By using these methods, we can learn more about the structure of the data and use that structure to make predictions and group the data.