Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to use Turing machines to recognize languages in TOC?
A Turing machine (TM) can be formally described as seven tuples −
(Q,X, ∑, δ,q0,B,F)
Where,
Q is a finite set of states.
X is the tape alphabet.
∑ is the input alphabet.
δ is a transition function: 𝛿:QxX->QxXx{left shift, right shift}.
q0 is the initial state.
B is the blank symbol.
F is the final state.
A Turing machine T recognises a string x (over ∑) if and only when T starts in the initial position and x is written on the tape,
T halts in a final state.
T is said to recognize a language A, if x is recognised by T and if and only if, x belongs to A.
Be aware that while running a TM, you can also read/write other symbols from/onto a tape, not necessarily only those from the alphabet A.
A Turing machine T does not recognize a string x, if T does not halt in a state that is not final.
There are TMs which for an input don’t halt at all and run forever.
Instantaneous Description
To describe the TM at a given time we need to understand three things, which are given below −
What is on the tape?
Where is the tape head?
What state is the control in?
We will represent this information as follows:
State i − B a a b a b B
Here, the B symbol represents an empty cell (repeated indefinitely to left and right) and the position of the tape head is in red.
Example
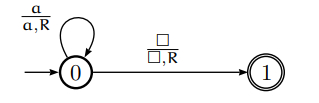
For ∑ = {a, b} design a Turing machine that accepts the language denoted by the regular expression a*.
Step 1 − Starting at the left end of the input, we read each symbol and check that it is a.
Step 2 − If it is, we continue moving right.
Step 3 − If we reach a blank symbol without encountering anything but a, we terminate and accept the string.
Step 4 − If the input contains a b anywhere (the string is not in L(a*)) we halt in a non-final state.
To keep track of the computation, two states 0 (initial) and 1 (final) are sufficient. As the transition function we can use −
T(0, a) = (0, a, R),
T(0,B ) = (1,B , R)
Or we can draw a figure −
736 Views
