Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to measure medium resistances? (Resistance Measurement Methods)
The resistances that range from about 1Ω to about 100 kΩ are classified as medium resistances. The resistances of most of electrical apparatus are the examples of medium resistances.
Measurement of Medium Resistances
To measure the medium resistances following methods are used −
Ammeter-Voltmeter Method
Substitution Method
Wheatstone Bridge
Carey-Foster Slide-Wire Bridge Method.
Ammeter-Voltmeter Method
In this method, current through the unknown resistor (Rx) and the potential drop across it are simultaneously measured. The readings are obtained by ammeter and voltmeters respectively. There are two ways in ammeter and voltmeters may be connected for measurement as,
Case 1 – When voltmeter is directly connected across the resistor, then the ammeter measures current flowing through the unknown resistance (Rx) and the voltmeter.
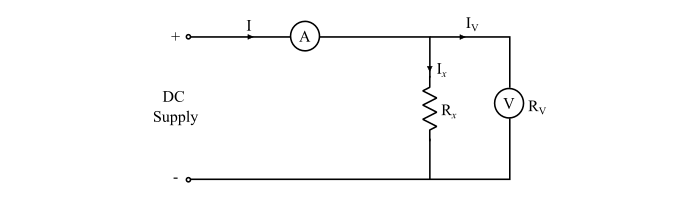
Current through ammeter = Current through(𝑅x) + Current through voltmeter
$$\mathrm{I=I_{R_{x}}+I_{V}}$$
$$\mathrm{\Rightarrow\:I_{R_{x}}=I-I_{V}}$$
Therefore, the value of unknown resistance,
$$\mathrm{R_{X}=\frac{V}{I_{X}}=\frac{V}{I-I_{V}}=\frac{V}{I-(V/R_{V})}\:\:\:...(1)}$$
Case 2 – When the ammeter is connected such that it measures only the current flowing through the unknown resistor (Rx), then the voltmeter measures voltage drop across the ammeter and Rx.
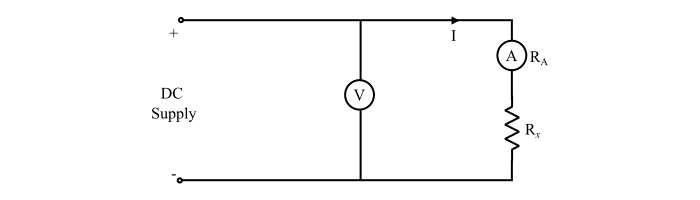
Therefore,
$$\mathrm{V=IR_{A}+IR_{X}=I(R_{A}+R_{X})}$$
$$\mathrm{\Rightarrow\:R_{X}=\frac{V}{I}-R_{A}\:\:\:\:...(2)}$$
Substitution Method
Step 1 – In this method, first the unknown resistance (Rx) is put into the circuit and note the value of current.
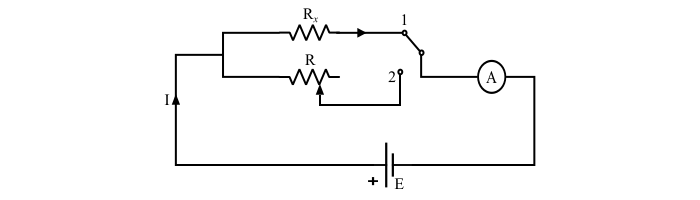
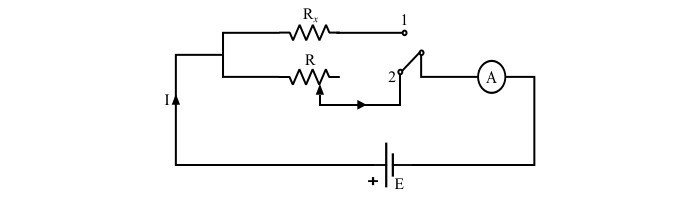
Step 2 – Then the resistance Rx is removed and it is substituted by a known variable resistance R which is varied so that the value of current is same in both the cases. This value of R is equal to the value of unknown resistance.
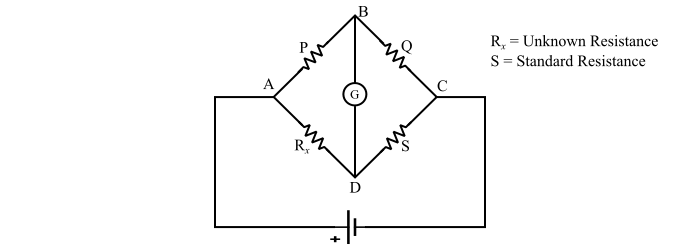
Wheatstone Bridge
The Wheatstone bridge method is the most accurate method for the measurement of resistances.
The bridge consists of four resistive arms, source of emf and a galvanometer (null detector). The current through the galvanometer depends upon the potential difference between the points B and D. The bridge is said to be balanced when the potential difference across the galvanometer is zero so that there is no current flows through the galvanometer.
For the balanced Wheatstone bridge,
$$\mathrm{PS=QR_{x}}$$
$$\mathrm{\Rightarrow\:R_{x}=\frac{PS}{Q}\:\:\:...(3)}$$
Carey-Foster Slide-Wire Bridge Method
The circuit of this bridge is the elaborated form of Wheatstone bridge and is specially used for comparing two nearly equal resistances.
The circuit consists of four resistive arms, where R1 and R2 are the ratio arms, R3 is standard resistance and Rx is unknown resistance. A slide-wire (m-n) of length l and uniform crosssection is connected between R3 and Rx. The slide wire has a resistance of r Ω per unit length.
The resistances R1 and R2 are adjusted so that the ratio $\mathrm{(\frac{R_{1}}{R_{2}})}$ is approximately equal to the ratio $\mathrm{(\frac{R_{x}}{R_{3}})}$. This balance is obtained by adjusting the sliding contact on the slide-wire. Then, For the first balance, let l1 is the distance of the sliding contact from the point m of the slide wire. Thus,
$$\mathrm{\frac{R_{1}}{R_{2}}=\frac{R_{x}+l_{1}r}{R_{3}+(l-l_{1})r}\:\:\:...(4)}$$
For the second balance, let l2 is the distance from the point m of the slide wire and the resistances Rx and R3 are interchanged, then
$$\mathrm{\frac{R_{1}}{R_{2}}=\frac{R_{3}+l_{2}r}{R_{x}+(l-l_{2})r}\:\:\:...(5)}$$
From eqns. (4) and (5), we get,
$$\mathrm{\frac{R_{x}+l_{1}r}{R_{3}+(l-l_{1})r}=\frac{R_{3}+l_{2}r}{R_{x}+(l-l_{2})r}}$$
Hence, the difference (R3 – Rx) is obtained from resistance of the slide wire between the two balance points.
Now, the value of r i.e. resistance per unit length of the slide wire is obtained by connecting a known high resistance in parallel with R3, that reduces the effective value to R3′, thus again repeat the above procedure to obtain new balance points 𝑙1′and 𝑙2′, so that,
$$\mathrm{R_{3}^{'}-R_{x}^{'}=r(l_{1}^{'}-l_{2}^{'})\:\:\:\:...(7)}$$
Dividing eqn. (6) by eqn. (7), we obtain,
$$\mathrm{\frac{R_{3}-R_{x}}{R_{3}^{'}-R_{x}^{'}}=\frac{r(l_{1}-l_{2})}{r(l_{1}^{'}-l_{2}^{'})}}$$
$$\mathrm{\Rightarrow\:R_{x}=\frac{R_{3}(l_{1}^{'}-l_{2}^{'})-R_{3}^{'}(l_{1}-l_{2})}{(l_{1}^{'}-l_{2}^{'}-l_{1}+l_{2})}\:\:\:\:....(8)}$$
4K+ Views
