Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to measure low resistances? (Resistance Measurement Methods)
The resistances of the values of less than or equal to 1 Ω are classified as low resistances. For example, the resistances of armatures and series windings of large machines, ammeter shunts, contacts, etc.
Measurement of Low Resistances
For the measurement of low resistances, the following methods are used −
Ammeter-Voltmeter Method
Potentiometer Method
Kelvin Double Bridge Method
Ammeter – Voltmeter Method
In this method, current through the unknown resistor (Rx) and the potential drop across it are simultaneously measured. The readings are obtained by ammeter and voltmeters respectively. There are two ways in ammeter and voltmeters may be connected for measurement as,
Case 1 – When voltmeter is directly connected across the resistor, then the ammeter measures current flowing through the unknown resistance (Rx) and the voltmeter.
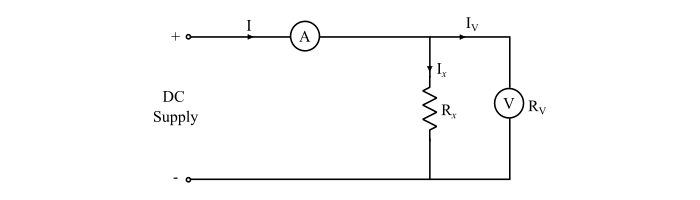
Current through ammeter = Current through(𝑅x) + Current through voltmeter
$$\mathrm{I=I_{R_{x}}+I_{V}}$$
$$\mathrm{\Rightarrow\:I_{R_{x}}=I-I_{V}}$$
Therefore, the value of unknown resistance,
$$\mathrm{R_{x}=\frac{V}{I_{x}}=\frac{V}{I-I_{V}}=\frac{V}{I-(V/R_{V})}\:\:\:...(1)}$$
Case 2 – When the ammeter is connected such that it measures only the current flowing through the unknown resistor (Rx), then the voltmeter measures voltage drop across the ammeter and Rx.
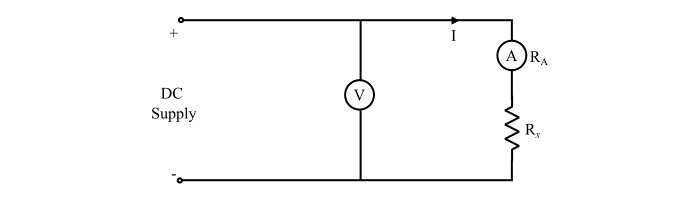
Therefore,
$$\mathrm{V=IR_{A}+IR_{x}=l(R_{A}+R_{x})}$$
$$\mathrm{\Rightarrow\:R_{x}=\frac{V}{l}-R_{A}\:\:\:...(2)}$$
Potentiometer Method
In the potentiometer method, the unknown resistance is compared with a standard resistance of the same order of magnitude.
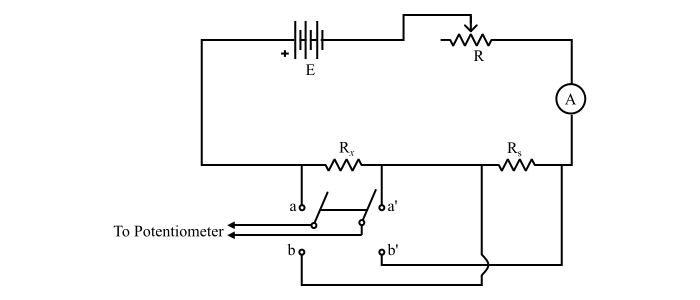
The circuit consists of an unknown resistance (Rx), a rheostat (R) and a standard resistance (Rs) all are connected in series across a low voltage, high current supply. The value of Rs should be known and of the same order of Rx. The current flowing in the circuit is adjusted,so that the potential difference across each resistor is about 1 V.
Now, the voltage drop across both the standard resistance (Rs) and unknown resistance (Rx) are measured by a potentiometer. The ratio of the two potentiometer readings gives the ratio of Rx and Rs, i.e.
$$\mathrm{\frac{R_{x}}{R_{s}}=\frac{V_{R_{x}}}{V_{R_{s}}}\:\:\:\:...(3)}$$
Kelvin Double Bridge Method
The Kelvin double bridge is a modified version of Wheatstone bridge and used to measure the low resistances with higher accuracy. This bridge is called double bridge since the circuit contains a second set of ratio arms (p and q). This second set of ratio arms connects the galvanometer (G) to a point f at the appropriate potential difference between c and d and this eliminates the effect of yoke resistance r. The galvanometer shows zero reading when potential at a equals to the potential at f, i.e. the bridge is balanced.
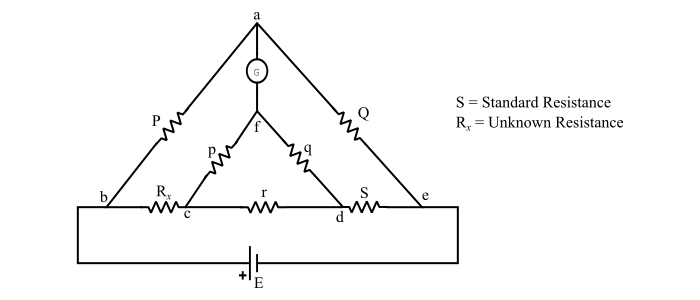
Therefore, the value of unknown resistance can be given by,
$$\mathrm{R_{x}=\frac{PS}{Q}+\frac{pr}{p+q+r}(\frac{P}{Q}-\frac{p}{q})}$$
Since, the ratio of resistances of arms p and q is the same as the ratio of P and Q. Thus,
$$\mathrm{\frac{p}{q}=\frac{P}{Q}}$$
Substituting in the above expression, we get,
$$\mathrm{R_{x}=\frac{PS}{Q}\:\:\:...(4)}$$
The eq. (4) is the work equation of kelvin double bridge.
5K+ Views
