Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to measure high resistances? (Resistance Measurement Methods)
Resistances of the order of 100 kΩ and upwards are classified as high resistances. For example, insulation resistances.
Measurement of High Resistances
The following methods are employed for the measurement of high resistances −
Direct Deflection Method
Loss of Charge Method
Megohm Bridge
Megger
Direct Deflection Method
In this method, a very sensitive and high resistance (more than 1 kΩ) PMMC galvanometer is connected in series with the resistance to be measured and to a battery. The deflection of galvanometer gives the measure of unknown resistance. This method is mainly used for the measurement of insulation resistance.
Let us take an example of direction deflection method for measuring insulation resistance of a cable.
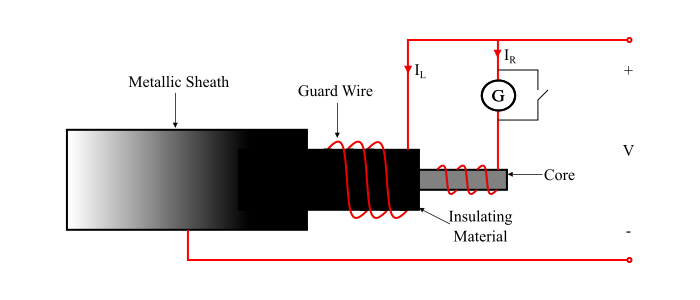
Refer the figure, the galvanometer (G) measures the current IR between conductor core and metal sheath. The leakage current IL over the surface of insulating material is carried by the guard wire wound on the insulation and does not flow through the galvanometer. Thus, the resistance of the cable is,
$$\mathrm{R=\frac{V}{I_{R}}\:\:\:\:...(1)}$$
Loss of Charge Method
The circuit arrangement for this method consists of a known capacitor (C), an electrostatic voltmeter (V) and an unknown resistance Rx.
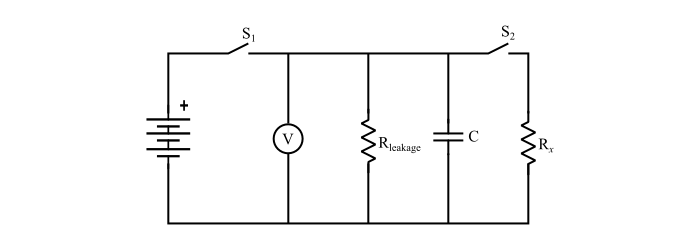
Step 1 – By closing the switch (S1), the capacitor (C) being charged by connecting a battery across it to a specific voltage.
Step 2 – Now, open the switch (S1) and close switch (S2), the capacitor is discharged through Rx and Rleakage. The time taken (t) for the potential difference to fall from V1 to V2 during discharge is observed by a stop watch.
From the circuit, the Req. is the effective resistance of Rx and Rleakage which are parallel connected.
$$\mathrm{\frac{1}{R_{eq.}}=\frac{1}{R_{x}}+\frac{1}{R_{𝑙𝑒𝑎𝑘𝑎𝑔𝑒}}}$$
As the discharging voltage equation of the capacitor is given by,
$$\mathrm{V_{2}=V_{1}e^{-t/CR_{eq.}}\:\:\:\:...(2)}$$
From the eqn. (2), Req. can be determined. Thus, by knowing the value of Req. and Rleakage, the value of unknown resistance Rx can be determined as
$$\mathrm{\frac{1}{R_{x}}=\frac{1}{R_{eq.}}-\frac{1}{R_{leakage}}\:\:\:...(3)}$$
Megohm Bridge
The circuit of Megohm bridge consists of power supplies, resistances, amplifiers and indicating instruments.
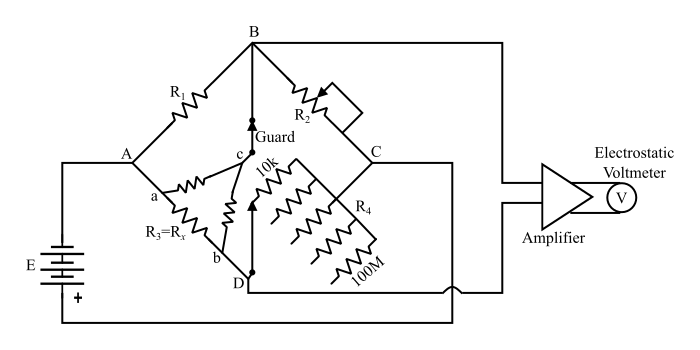
In this instrument, the dial on R2 is calibrated 1-10-100-1000 MΩ and the R4 gives five multipliers 0.1, 1, 10, 100 and 100. The junction of R1 and R2 is brought on the main panel and assigned a name as Guard terminal. The unknown resistance is given by,
$$\mathrm{R_{3}=\frac{R_{1}R_{4}}{R_{2}}\:\:\:\:...(4)}$$
Megger
Megger (megohmmeter) is a device used for the measurement of high resistances, mainly insulation resistances of electric circuits with respect to earth or one another. A megger consists of a source of emf and a voltmeter whose scale is usually calibrated in mega-ohms. The unknown resistance Rx has to be connected across the leads of megger.
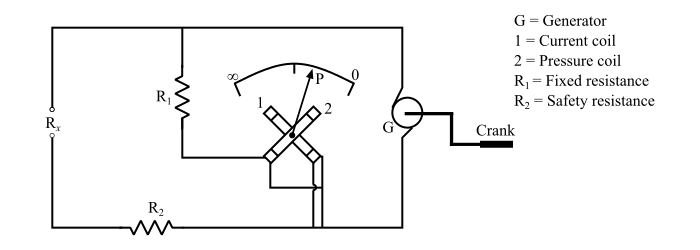
When the megger operates, the deflection of the moving system depends upon the ratio of the applied voltage and the current in the coils of the megger. The unknown resistance is read directly from the scale of the megger.
5K+ Views
