Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to Calculate the Capacitance of Different Types of Capacitors?
Capacitance - Definition
The ability of a capacitor to store charge is known as its capacitance. In other word, the capacitance can also be defined as the property of a material by virtue of it opposes the any change in voltage applied across it.
Capacitance: Formula
Experimentally, it has been found that, the charge Q stored in a capacitor is directly proportional to the voltage across it, i.e.
$$Q\propto\:V$$
$$Q=CV$$
Where, C is a constant and is called as capacitance of the capacitor.
$$\Rightarrow\:C=\frac{Q}{V}$$
Thus, the capacitance (C) of a capacitor can also be defined as the ratio of the charge on the either plate to the voltage across it.
Unit of Capacitance
We have seen that,
$$C=\frac{Q}{V}=\frac{Coulomb}{Volt}=Farad$$
The SI unit of capacitance is coulomb/volt which is also known as farad and denoted by F.
Equivalent Capacitance
Case 1 – When capacitors are connected in series
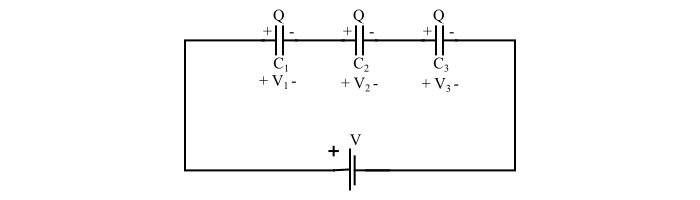
By referring the circuit, we can write,
$$V=V_{1}+V_{2}+V_{3}=(\frac{Q}{C_{1}}+\frac{Q}{C_{2}}+\frac{Q}{C_{3}})=Q(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}})$$
$$\Rightarrow\:\frac{V}{Q}=(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}})$$
$$\Rightarrow\frac{1}{C_{r}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}$$
From this equation, the total equivalent capacitance of series connected capacitors can be determined.
Case 2 – When capacitors are connected in parallel
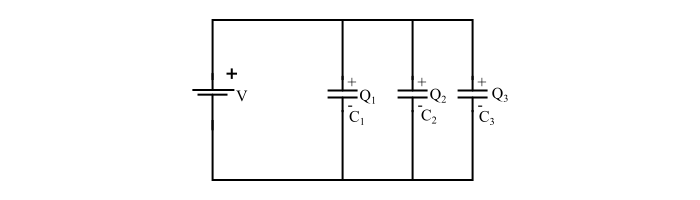
By referring the circuit, it can be written,
$$Q=Q_{1}+Q_{2}+Q_{3}=C_{1}V+C_{2}V+C_{3}V=V(C_{1}+C_{2}+C_{3})$$
$$\Rightarrow\:\frac{Q}{V}=(C_{1}+C_{2}+C_{3})$$
$$\Rightarrow\:C_{r}=C_{1}+C_{2}+C_{3}$$
The above equation gives the total capacitance of parallel connected capacitors.
Capacitance of a Parallel Plate Capacitor
Case 1 – With uniform dielectric medium
Consider a parallel plate capacitor consisting of two plates, each of surface area A. The plates are separated by a distance d. Air is present in between the plates as the dielectric medium.
Therefore, the capacitance of a parallel plate capacitor is,
Directly proportional to the surface area (A) of each plate.
Inversely proportional to the distance (d) between the plates.
Thus,
$$Capacitance,C\propto\:\frac{A}{d}$$
$$\Rightarrow\:C=\varepsilon_{0}\frac{A}{d}$$
Where, ε0 is the constant of proportionality and is known as absolute permittivity of vacuum or air and its value is equal to 8.854 × 10−12 F/m .
If there is a uniform dielectric material is placed between the plates of the capacitor, then capacitance of the capacitor becomes,
$$C=\varepsilon_{0}\varepsilon_{r}\frac{A}{d}$$
Where, εr is the relative permittivity of the dielectric material.
Case 2 – With composite dielectric medium
Consider the space between the plates of the capacitor is occupied by three dielectric materials of thickness d1, d2 and d3 and the relative permittivity εr1, εr2 and εr3 respectively. Then, the capacitance of individual section is given as,
$$C_{1}=\varepsilon_{0}\varepsilon_{r1}\frac{A}{d_{1}}\:;\:C_{2}=\varepsilon_{0}\varepsilon_{r2}\frac{A}{d_{2}}\:and\:C_{3}=\varepsilon_{0}\varepsilon_{r3}\frac{A}{d_{3}}$$
As from the figure, the three capacitances are appearing as they are connected in series, so
$$\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{(\varepsilon_{0}\varepsilon_{r1}\frac{A}{d_{1}})}+\frac{1}{(\varepsilon_{0}\varepsilon_{r2}\frac{A}{d_{2}})}+\frac{1}{(\varepsilon_{0}\varepsilon_{r3}\frac{A}{d_{3}})}$$
$$\Rightarrow\frac{1}{C}=\frac{d_{1}}{\varepsilon_{0}\varepsilon_{r1}A}+\frac{d_{2}}{\varepsilon_{0}\varepsilon_{r2}A}+\frac{d_{3}}{\varepsilon_{0}\varepsilon_{r3}A}=\frac{1}{\varepsilon_{0}A}(\frac{d_{1}}{\varepsilon_{r1}}+\frac{d_{2}}{\varepsilon_{r2}}+\frac{d_{3}}{\varepsilon_{r3}})$$
$$C=\frac{\varepsilon_{0}A}{(\frac{d_{1}}{\varepsilon_{r1}}+\frac{d_{2}}{\varepsilon_{r2}}+\frac{d_{3}}{\varepsilon_{r3}})}$$
$$In\:general,C=\frac{\varepsilon_{0}A}{\sum(\frac{d}{\varepsilon_{r}})}$$
Capacitance of Multiplate Capacitor
In order to obtain larger capacitance value, multiplate construction is employed. In this construction, the capacitor is built of alternate metal plates and thin sheets of dielectric. The odd numbered of plates are connected together to form one terminal A and even numbered plates are connected together to form the second terminal B.
Refer the figure of a multiplate (in this case 7 plates) capacitor, which is equivalent to 6 capacitors in parallel. Therefore, the total capacitance will be 6 times the capacitance of a single capacitor. If there are n plates, then (n – 1) capacitors will be in parallel. Therefore,
$$Capacitance\:of\:n-plate\:capacitor=(n-1)\frac{\varepsilon_{0}\varepsilon_{r}A}{d}$$
Where,
A is the area of each plate,
d is the distance between any two adjacent plates.
Capacitance of a Cylindrical Capacitor
A cylindrical capacitor (e.g. a cable) consists of two coaxial cylinders separated by a dielectric medium.
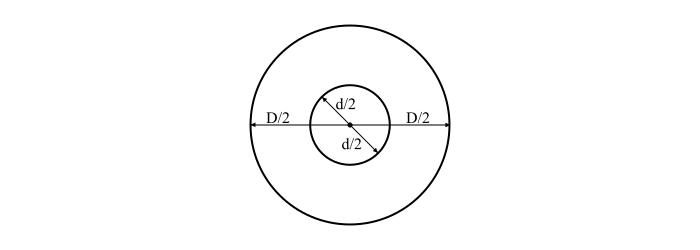
By referring the figure, the capacitance per unit length of cylindrical capacitor is given by,
$$C=\frac{2\pi\:\varepsilon_{0}\varepsilon_{r}}{log_{e}(\frac{D}{d})}\:F/m$$
If the length of cable (cylindrical capacitor) is l meters, then the capacitance of the cable is
$$C=\frac{2\pi\:\varepsilon_{0}\varepsilon_{r}l}{log_{e}(\frac{D}{d})}\:Farad$$
641 Views
