Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Graph k-NN decision boundaries in Matplotlib
To make graph k-NN decision boundaries in matplotlib, we can take the following Steps.
Steps
Set the figure size and adjust the padding between and around the subplots.
Initialize a variable n_neighbors for number of neighbors.
Load and return the iris dataset (classification).
Create x and y data points.
Make lists of dark and light colors.
Classifier implementing the k-nearest neighbors vote.
Create xmin, xmax, ymin and ymax data points.
Create a new figure or activate an existing figure.
Create a contourf plot.
Create a scatter plot with X dataset.
Set x and y axes labels, titles and scale of the axes.
To display the figure, use Show() method.
Example
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
plt.rcParams["figure.figsize"] = [7.00, 3.50]
plt.rcParams["figure.autolayout"] = True
n_neighbors = 15
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
h = .02
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])
cmap_bold = ['darkorange', 'c', 'darkblue']
clf = neighbors.KNeighborsClassifier(n_neighbors, weights='uniform')
clf.fit(X, y)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure()
plt.contourf(xx, yy, Z, cmap=cmap_light)
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=iris.target_names[y],
palette=cmap_bold, alpha=1.0, edgecolor="black")
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, 'uniform' = '%s')"
% (n_neighbors, 'uniform'))
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
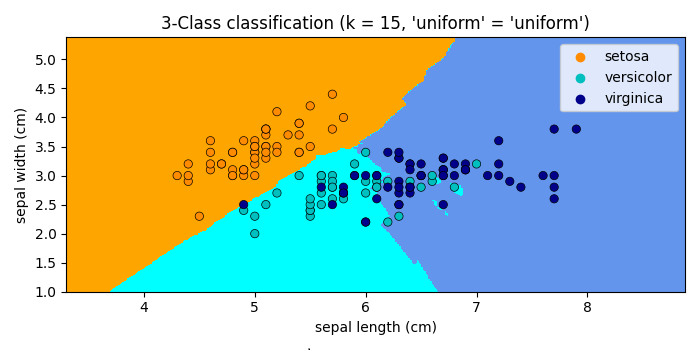
plt.Show()Output
It will produce the following output −
Updated on: 08-Oct-2021
5K+ Views
Advertisements