Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Breadth-first search traversal in Javascript
BFS visits the neighbor vertices before visiting the child vertices, and a queue is used in the search process. Following is how a BFS works −
- Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
- If no adjacent vertex is found, remove the first vertex from the queue.
- Repeat Rule 1 and Rule 2 until the queue is empty.
Let us look at an illustration of how BFS Traversal works:
Step | Traversal | Description |
|---|---|---|
1 | 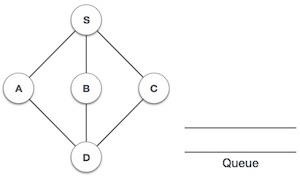 | Initialize the queue. |
2 | 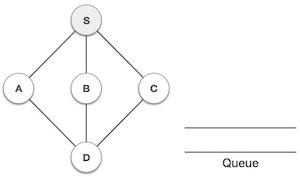 | We start by visiting S (starting node) and mark it as visited. |
3 | 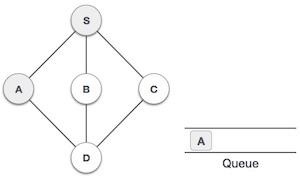 | We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it. |
4 | 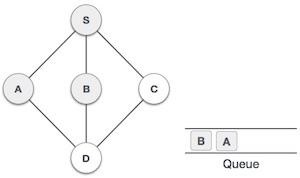 | Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it. |
5 | 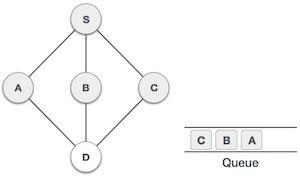 | Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it. |
6 | 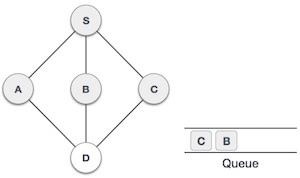 | Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A. |
7 |  | From A we have D as an unvisited adjacent node. We mark it as visited and enqueue it. |
At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.
Let's look at how we can implement this in JavaScript.
Example
BFS(node) {
// Create a Queue and add our initial node in it
let q = new Queue(this.nodes.length);
let explored = new Set();
q.enqueue(node);
// Mark the first node as explored explored.
add(node);
// We'll continue till our queue gets empty
while (!q.isEmpty()) {
let t = q.dequeue();
// Log every element that comes out of the Queue
console.log(t);
// 1. In the edges object, we search for nodes this node is directly connected to.
// 2. We filter out the nodes that have already been explored.
// 3. Then we mark each unexplored node as explored and add it to the queue.
this.edges[t]
.filter(n => !explored.has(n))
.forEach(n => {
explored.add(n);
q.enqueue(n);
});
}
}You can test this function using −
Example
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C");
g.addEdge("A", "B");
g.addEdge("A", "D");
g.addEdge("D", "E");
g.addEdge("E", "F");
g.addEdge("B", "G");
g.BFS("A");Output
This will give the output −
A C B D G E F
Updated on: 15-Jun-2020
4K+ Views
Advertisements