
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain Superposition Theorem
The superposition theorem is used in solving a network in which two or more sources are present and connected not in series or in parallel.
Statement of Superposition Theorem
If two or more voltage or current sources are acting simultaneously in a linear network, the resultant current in any branch is the algebraic sum of the currents that would be produced in it, when each source acts alone and all other independent sources are replaced by their internal resistances.
Explanation of Superposition Theorem
In the circuit given below, we have to find the branch currents viz. i1, i2, i3 by using superposition theorem.
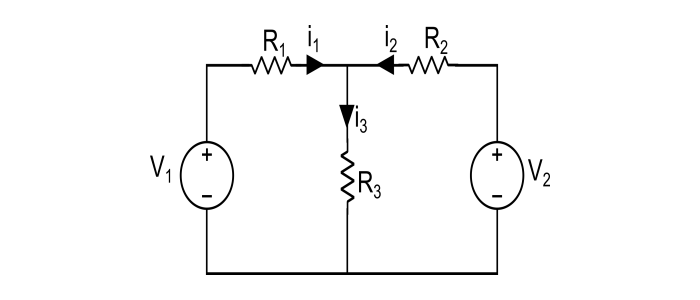
Step 1 – Take the source V1 alone at first, replacing V2 by short circuit.
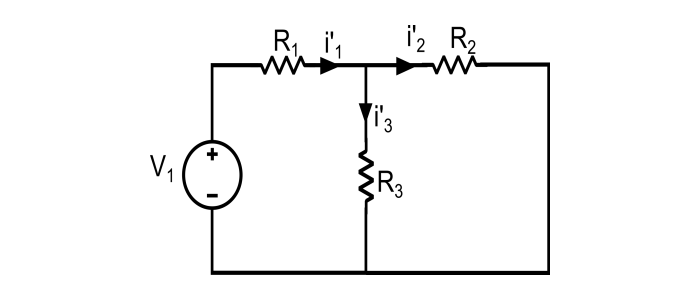
Here, the branch current i’1, i’2, i’3 are,
$$i'_{1}=\frac{V_{1}}{\frac{R_{2}R_{3}}{R_{2}+R_{3}}+R_{1}}$$
$$i'_{2}=i'_{1}\frac{R_{3}}{R_{2}+R_{3}}$$
$$i'_{3}=i'_{1}-i'_{2}$$
Step 2 – Take the source V2 alone, and replacing the V1 by short circuit.
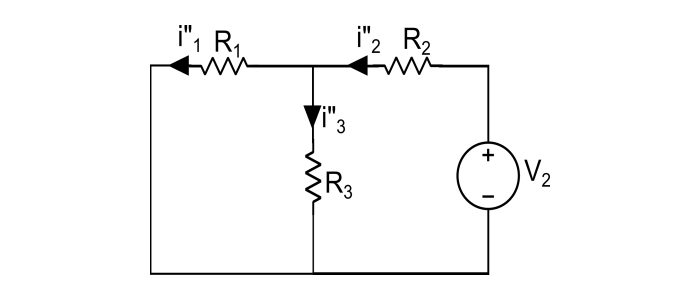
Here, the branch currents i"1, i"2, i"3 are,
$$i"_{2}=\frac{V_{2}}{\frac{R_{1}R_{3}}{R_{1}+R_{3}}+R_{2}}$$
$$i"_{2}=i"_{2}\frac{R_{3}}{R_{1}+R_{3}}$$
$$i"_{3}=i"_{2}-i"_{1}$$
Step 3 – By applying superposition theorem,
$$i_{1}=i'_{1}-i"_{1}$$
$$i_{2}=i"_{2}-i'_{1}$$
$$i_{3}=i'_{3}+i"_{3}$$
Note – During the application of superposition theorem, the direction of currents calculated for each source should be taken care of.
Steps for Solution of a Network using Superposition Theorem
Step 1 – Take only one independent source and deactivate the other independent sources (Voltage source replaced by a short circuit and current source is replaced by an open circuit). Obtain the branch currents.
Step 2 – Repeat the step 1 for each of the independent sources.
Step 3 – To determine the net branch current using superposition theorem, add the currents obtained in the step 1 and step 2 for each branch. If the currents obtained in step 1 and step 2 are in same direction then add then and if the respective currents are in the opposite direction in each step, then take the direction of original current as reference and subtract the current of opposite direction. The net current in each branch is then calculated.
Numerical Example
In circuit given below, Vs = 0, I = 4 A; find I when Vs = 20 V.
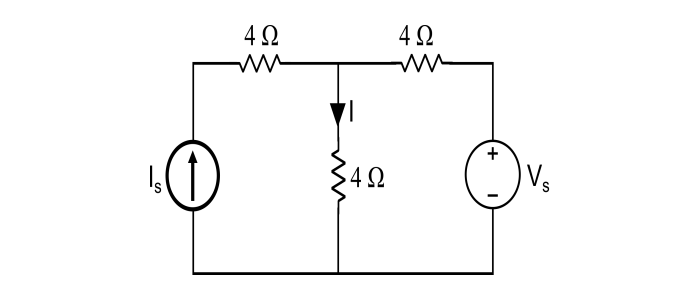
Solution
Step 1 – When Vs = 0 i.e. short circuited and Is acting alone then,
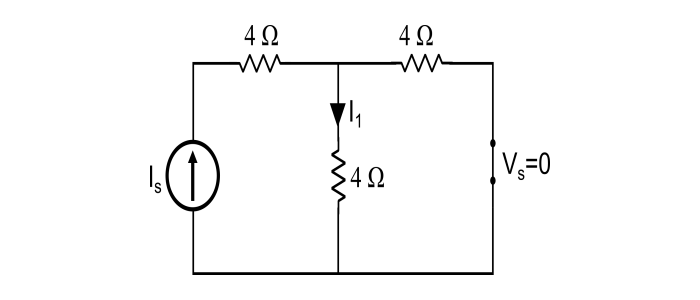
$$I_{1}=4A\:(given)$$
Step 2 – When Vs =20 V and Is is deactivated, then
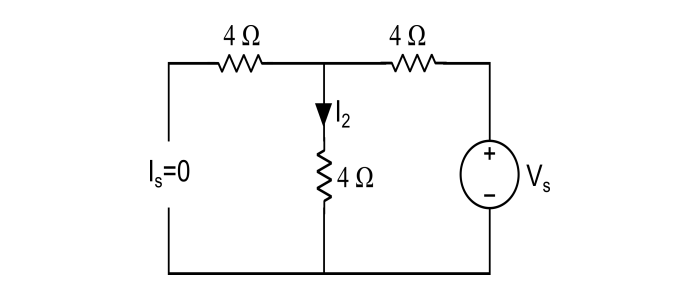
$$I_{2}=\frac{20}{4+4}=2.5A$$
Therefore, by applying superposition theorem, the net current (I) is,
$$I=I_{1}+I_{2}=4+2.5=6.5A$$

