Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum Power Transfer Theorem
The maximum power theorem (MPT) is used to find the value of load resistance for which there would be maximum amount of power transfer from the source to load.
Statement of MPT
A resistive load that is connected to a DC source, receives maximum power when the load resistance is equal to the internal resistance of the source as seen from the load terminals.
Explanation of MPT
Consider the following circuit diagram to determine the value of RL such that it receives maximum power from the DC source.
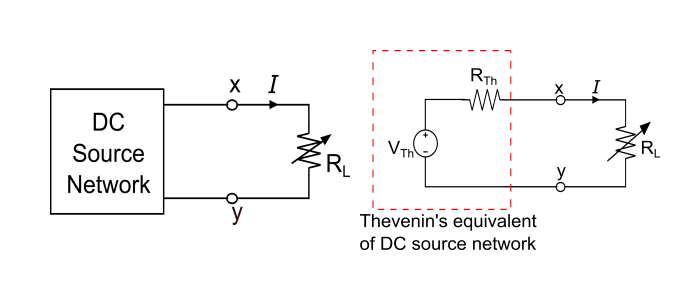
The load current is,
$$I=\frac{V_{Th}}{R_{Th}+R_{L}}$$
Thus, the power delivered to the resistive load is,
$$P_{L}=I^{2}R_{L}=(\frac{V_{Th}}{R_{Th}+R_{L}})^{2}R_{L}$$
As we know, the load resistance is variable. Thus, PL can be maximised by varying RL.
$$\Rightarrow\:P_{L}=\frac{V_{Th}^{2}R_{L}}{(R_{th}+R_{L})^{2}}=\frac{V_{Th}^{2}R_{L}}{R_{Th}^{2}+R_{L}^{2}+2R_{Th}R_{L}}$$
$$\Rightarrow\:P_{L}=\frac{V_{Th}^{2}}{(\frac{R_{th}^{2}}{R_{L}}+R_{L}+2R_{Th})}=\frac{V_{Th}^{2}}{D}$$
In order to PL be maximum the denominator (D) term should be minimum, i.e.,
$$\frac{dD}{dR_{L}}=0$$
$$\frac{d}{dR_{L}}(\frac{R_{Th}^{2}}{R_{L}}+R_{L}+2R_{Th})=0$$
By solving the above differential equation, we get,
$$R_{L}=R_{Th}$$
Hence, maximum power will deliver to the load if the load resistance is equal to internal resistance of the source network i.e.
Load Resistance = Internal Resistance of the source
Amount of Maximum Power (Pmax)
$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}$$
Here, Pmax is the amount of maximum power consumed by the load.
The total power supplied by the source is
$$P=2\frac{V_{Th}^{2}}{4R_{Th}}=\frac{V_{Th}^{2}}{2R_{Th}}$$
The efficiency of the circuit during maximum power transfer becomes,
$$\eta=\frac{P_{max}}{P}\times\:100=50$$%
Steps for Solution of Network using MPT
step 1 – Remove the load resistance and replace all the independent sources by their internal resistance and determine the RTh of the source network looking through the open circuited load terminals.
Step 2S – As per MPT, the value of RTh gives the value of load resistance RL i.e. RTh = RL, that allows maximum power transfer.
Step 3 – Find the value of VTh across the open circuited load terminals.
Step 4 – The amount maximum power transferred is given by,
$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}$$
Numerical Example
Find the value of load resistance RL in the circuit given below such that maximum power transfer takes place. Also, calculate the amount of maximum power.
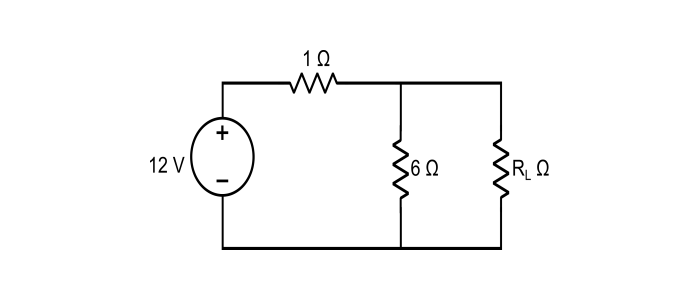
Solution
Step 1 – Remove the load resistance and replace all the independent sources by their internal resistance (in this case, 12 V ideal voltage source is short circuited) and determine the value of RTh that give RL corresponding to the maximum power transfer.
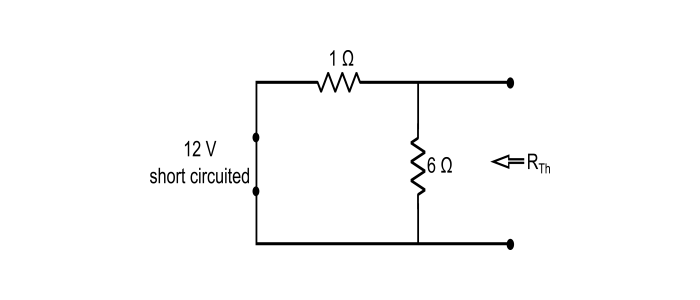
$$R_{Th}=1\:\Omega\:\lVert\:6\:\Omega=\frac{1\times\:6}{1+\:6}=\frac{6}{7}\:\Omega$$
As per maximum power transfer theorem,
$$R_{L}=R_{Th}=\frac{6}{7}\:\Omega$$
Step 2 – Determine the VTh across the open circuited load terminals,
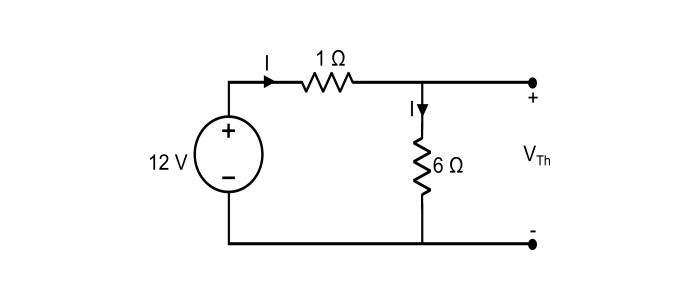
Here, the current in the circuit is,
$$I=\frac{12}{1+6}=\frac{12}{7}\:Ampere$$
As, the load terminal is open circuited, hence the VTh is the voltage drop across the 6 Ω resistor. Thus,
$$V_{Th}=I\times\:6\Omega=\frac{12}{7}\times\:6=\frac{72}{7}\:Volt$$
The amount of maximum power delivered to the load is,
$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}=\frac{(72/7)^{2}}{4\times\:(6/7)}=30.857W$$
Hence, the value of load resistance for maximum power transfer is equal to (6/7 Ω ) and the amount of maximum power delivered to the load is 30.857 Watt.
441 Views
