Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Definition and Properties of Trees
Tree is a discrete structure that represents hierarchical relationships between individual elements or nodes. A tree in which a parent has no more than two children is called a binary tree.
Tree and its Properties
Definition − A Tree is a connected acyclic undirected graph. There is a unique path between every pair of vertices in G. A tree with N number of vertices contains (N-1) number of edges. The vertex which is of 0 degree is called root of the tree. The vertex which is of 1 degree is called leaf node of the tree and the degree of an internal node is at least 2.
Example − The following is an example of a tree −
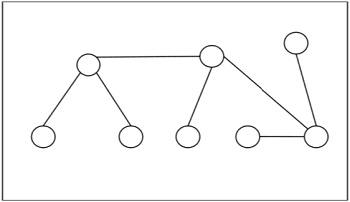
Centers and Bi-Centers of a Tree
The center of a tree is a vertex with minimal eccentricity. The eccentricity of a vertex X in a tree G is the maximum distance between the vertex X and any other vertex of the tree. The maximum eccentricity is the tree diameter. If a tree has only one center, it is called Central Tree and if a tree has only more than one centers, it is called Bi-central Tree. Every tree is either central or bi-central.
Labeled Trees
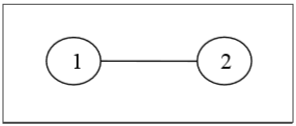
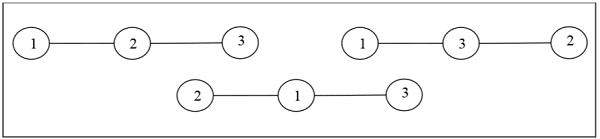
Definition − A labeled tree is a tree the vertices of which are assigned unique numbers from 1 to n. We can count such trees for small values of n by hand so as to conjecture a general formula. The number of labeled trees of n number of vertices is nn-2. Two labeled trees are isomorphic if their graphs are isomorphic and the corresponding points of the two trees have the same labels.
Example
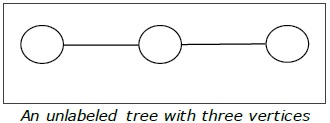
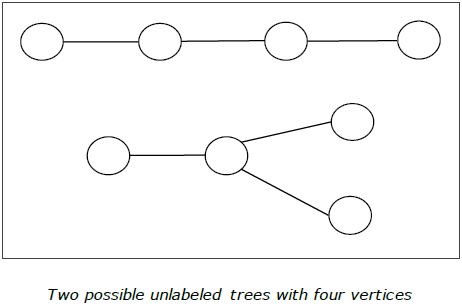
Unlabeled Trees
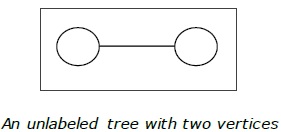
Definition − An unlabeled tree is a tree the vertices of which are not assigned any numbers. The number of labeled trees of n number of vertices is $\frac {(2n)!}{ (n+1)!n! }$ (nth Catalan number)
Example
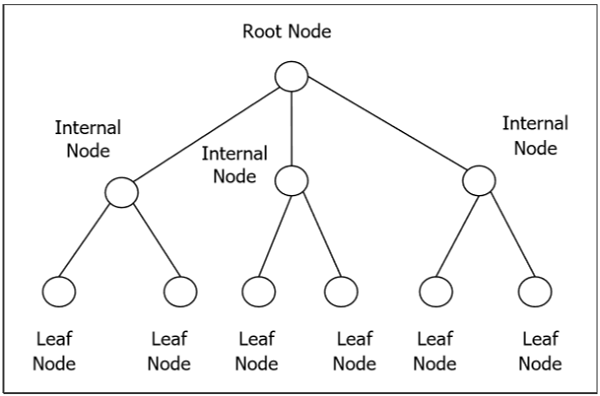
Rooted Tree
A rooted tree G is a connected acyclic graph with a special node that is called the root of the tree and every edge directly or indirectly originates from the root. An ordered rooted tree is a rooted tree where the children of each internal vertex are ordered. If every internal vertex of a rooted tree has not more than m children, it is called an m-ary tree. If every internal vertex of a rooted tree has exactly m children, it is called a full m-ary tree. If m = 2, the rooted tree is called a binary tree.
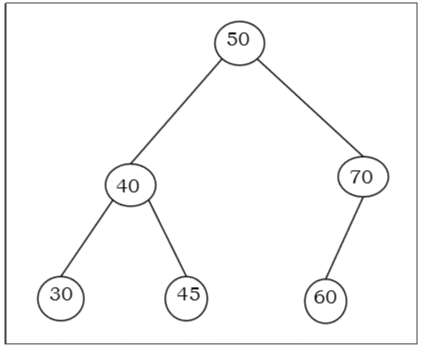
Binary Search Tree
Binary Search tree is a binary tree which satisfies the following property −
- X in left sub-tree of vertex V, Value(X) ≤ Value (V)
- Y in right sub-tree of vertex V, Value(Y) ≥ Value (V)
So, the value of all the vertices of the left sub-tree of an internal node V are less than or equal to V and the value of all the vertices of the right sub-tree of the internal node V are greater than or equal to V. The number of links from the root node to the deepest node is the height of the Binary Search Tree.
Example
Algorithm to search for a key in BST
BST_Search(x, k) if ( x = NIL or k = Value[x] ) return x; if ( k < Value[x]) return BST_Search (left[x], k); else return BST_Search (right[x], k)
Complexity of Binary search tree
| Average Case | Worst case | |
|---|---|---|
| Space Complexity | O(n) | O(n) |
| Search Complexity | O(log n) | O(n) |
| Insertion Complexity | O(log n) | O(n) |
| Deletion Complexity | O(log n) | O(n) |
11K+ Views
To Continue Learning Please Login