Decoder: Definition and Applications

What is a Decoder?

In digital electronics, a combinational logic circuit that converts an N-bit binary input code into M output channels in such a way that only one output channel is activated for each one of the possible combinations of inputs is known as a decoder.

In other words, a combinational logic circuit which converts N input lines into a maximum of 2_N output lines is called a decoder.

Therefore, a decoder is a combination logic circuit that is capable of identifying or detecting a particular code. The operation that a decoder performs is referred to as decoding. A general block diagram of a decoder is shown in Figure-1.

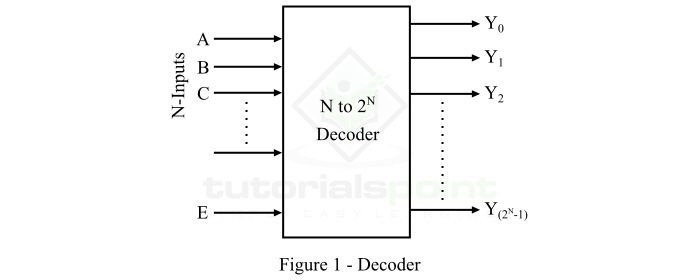
Here, the decoder has N input lines and M (2^N) output lines. In a decoder, each of the N input lines can be a 0 or a 1, hence the number of possible input combinations or codes be equal to 2^N. For each of these input combinations, only one of the M output lines will be active, and all other output lines will remain inactive.

Types of Decoders

There are several types of decoder present. But, based on the input and output lines present, decoders may classified into the following three types −

• 2 to 4 Decoder
• 3 to 8 Decoder
• 4 to 16 Decoder

Now, let us discuss each type of decoder in detail one by one.

2 to 4 Decoder

The 2 to 4 decoder is one that has 2 input lines and 4 (2²) output lines. The functional block diagram of the 2 to 4 decoder is shown in Figure-2.

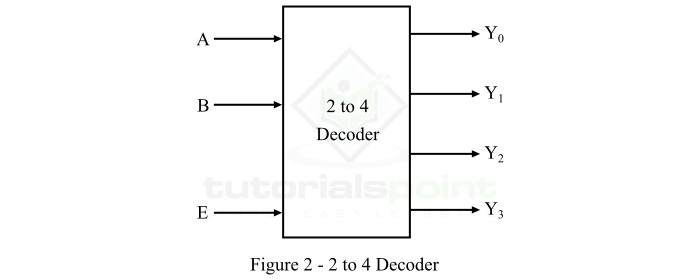
When this decoder is enabled with the help of enable input E, then its one of the four outputs will be active for each combination of inputs. The operation of this 2-line to 4-line decoder can be analyzed with the help of its truth table which is given below.

Inputs			Outputs
E	A	B	Y3	Y2	Y1	Y0
0	X	X	0	0	0	0
1	0	0	0	0	0	1
1	0	1	0	0	1	0
1	1	0	0	1	0	0
1	1	1	1	0	0	0

Using this truth table, we can derive the Boolean expression for each output as follows −

$$Y_{0}=E\cdot \bar{A}\cdot \bar{B}$$

$$Y_{1}=E\cdot \bar{A}\cdot B$$

$$Y_{2}=E\cdot A \cdot \bar{B}$$

$$Y_{3}=E\cdot A \cdot B$$

As each output term contains products of input variables that can be implemented with the help of AND gates. Therefore, the logic circuit diagram of the 2 to 4 decoder is shown in Figure-3.

Operation − The operation of logic circuit of the 2 to 4 decoder is described as follows −

• When enable input (E) is inactive, i.e. set to 0, none of the AND gates will function.

• When enable input (E) is made active by setting it to 1, then the circuit works as explained below.

• When A = 0 and B = 0, the AND gate 1 becomes active and produces output Y₀.

• When A = 0 and B = 1, the AND gate 2 becomes active and produces output Y₁.

• When A = 1 and B = 0, the AND gate 3 becomes active and produces output Y₂.

• When A = 1 and B = 1, the AND gate 4 becomes active and produces output Y₃.

3 to 8 Decoder

The 3 to 8 decoder is one that has 3 input lines and 8 (2³) output lines. The functional block diagram of the 3 to 8 decoder is shown in Figure-4.

When this decoder is enabled with the help of enable input E, then it's one of the eight outputs will be active for each combination of inputs. The operation of this 3-line to 8-line decoder can be analyzed with the help of its function table which is given below.

Inputs				Outputs
E	A	B	C	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
0	X	X	X	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0	1
1	0	0	1	0	0	0	0	0	0	1	0
1	0	1	0	0	0	0	0	0	1	0	0
1	0	1	1	0	0	0	0	1	0	0	0
1	1	0	0	0	0	0	1	0	0	0	0
1	1	0	1	0	0	1	0	0	0	0	0
1	1	1	0	0	1	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0	0

Using this function table, we can derive the Boolean expression for each output as follows −

$$Y_{0}=E\bar{A}\bar{B}\bar{C}$$

$$Y_{1}=E\bar{A}\bar{B}C$$

$$Y_{2}=E\bar{A}B\bar{C}$$

$$Y_{3}=E\bar{A}BC$$

$$Y_{4}=EA\bar{B}\bar{C}$$

$$Y_{5}=EA\bar{B}C$$

$$Y_{6}=EAB\bar{C}$$

$$Y_{7}=EABC$$

As we can see, each output term contains products of input variables, hence they can be implemented with the help of AND gates. Therefore, the logic circuit diagram of the 3 to 8 decoder is shown in Figure-5.

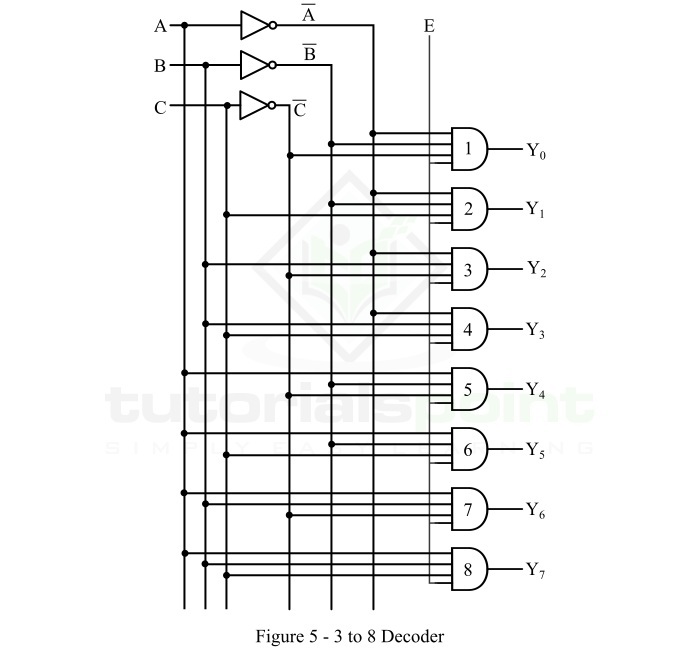
Operation − The operation of logic circuit of the 3 to 8 decoder is described as follows −

• When enable input (E) is inactive, i.e. set to 0, none of the AND gates will function.

• When enable input (E) is made active by setting it to 1, then the circuit works as described below.

• When A = 0, B = 0, and C = 0, the AND gate 1 becomes active and produces output Y₀.

• When A = 0, B = 0, and C = 1, the AND gate 2 becomes active and produces output Y₁.

• When A = 0, B = 1, and C = 0, the AND gate 3 becomes active and produces output Y₂.

• When A = 0, B = 1, and C = 1, the AND gate 4 becomes active and produces output Y₃.

• When A = 1, B = 0, and C = 0, the AND gate 5 becomes active and produces output Y₄.

• When A = 1, B = 0, and C = 1, the AND gate 6 becomes active and produces output Y₅.

• When A = 1, B = 1, and C = 0, the AND gate 7 becomes active and produces output Y₆.

• When A = 1, B = 1, and C = 1, the AND gate 8 becomes active and produces output Y₇.

4 to 16 Decoder

The 4 to 16 decoder is the type of decoder which has 4 input lines and 16 (2¹⁴) output lines. The functional block diagram of the 4 to 16 decoder is shown in Figure-6.

When this decoder is enabled with the help of enable input E, it's one of the sixteen outputs will be active for each combination of inputs. The operation of the 4-line to 16-line decoder can be analyzed with the help of its function table which is given below.

Inputs					Output
E	A	B	C	D
0	X	X	X	X	0
1	0	0	0	0	Y0
1	0	0	0	1	Y1
1	0	0	1	0	Y2
1	0	0	1	1	Y3
1	0	1	0	0	Y4
1	0	1	0	1	Y5
1	0	1	1	0	Y6
1	0	1	1	1	Y7
1	1	0	0	0	Y8
1	1	0	0	1	Y9
1	1	0	1	0	Y10
1	1	0	1	1	Y11
1	1	1	0	0	Y12
1	1	1	0	1	Y13
1	1	1	1	0	Y14
1	1	1	1	1	Y15

From this function table, we can directly write the Boolean expression for each output as follows −

$$Y_{0}=E\bar{A}\bar{B}\bar{C}\bar{D}$$

$$Y_{1}=E\bar{A}\bar{B}\bar{C}D$$

$$Y_{2}=E\bar{A}\bar{B}C\bar{D}$$

$$Y_{3}=E\bar{A}\bar{B}CD$$

$$Y_{4}=E\bar{A}B\bar{C}\bar{D}$$

$$Y_{5}=E\bar{A}B\bar{C}D$$

$$Y_{6}=E\bar{A}BC\bar{D}$$

$$Y_{7}=E\bar{A}BCD$$

$$Y_{8}=EA\bar{B}\bar{C}\bar{D}$$

$$Y_{9}=EA\bar{B}\bar{C}D$$

$$Y_{10}=EA\bar{B}C\bar{D}$$

$$Y_{11}=EA\bar{B}CD$$

$$Y_{12}=EAB\bar{C}\bar{D}$$

$$Y_{13}=EAB\bar{C}D$$

$$Y_{14}=EABC\bar{D}$$

$$Y_{15}=EABCD$$

We can implement these output expression in the same way as we done for the 2 to 4 decoder and 3 to 8 decoder.

Now, let us discuss the applications of decoders.

Applications of Decoders

Decoders are used in the cases where an output or a collection of outputs is to be activated only on the occurrence of a particular combination of input codes. Some important applications of decoders are listed below −

• Decoders are used for code conversions.

• Decoders are extensively used in memory systems of computers.

• Decoders are also used for de-multiplexing or data distribution.

• Decoders are also used in data routing applications where very short propagation delay is required.

• Decoder may also be used for timing or sequencing purposes.

• Decoders are also utilized to turn on and off digital devices at a specific time.

This is all about decoder and its applications in digital electronic systems.